NCERT Solution for Class 10 Mathematics Chapter 6 - Triangles
Excercise 6.1
Question 1
Fill in the blanks using correct word given in the brackets:-
(i) All circles are __________. (congruent, similar)
(ii) All squares are __________. (similar, congruent)
(iii) All __________ triangles are similar. (isosceles, equilateral)
(iv) Two polygons of the same number of sides are similar, if (a) their corresponding angles are __________ and (b) their corresponding sides are __________. (equal, proportional)
(i) All circles are __________. (congruent, similar)
(ii) All squares are __________. (similar, congruent)
(iii) All __________ triangles are similar. (isosceles, equilateral)
(iv) Two polygons of the same number of sides are similar, if (a) their corresponding angles are __________ and (b) their corresponding sides are __________. (equal, proportional)
Solution 1
(i) All circles are SIMILAR.
(ii) All squares are SIMILAR.
(iii) All EQUILATERAL triangles are similar.
(iv) Two polygons of same number of sides are similar, if their corresponding angles are EQUAL and their corresponding sides are PROPORTIONAL.
(ii) All squares are SIMILAR.
(iii) All EQUILATERAL triangles are similar.
(iv) Two polygons of same number of sides are similar, if their corresponding angles are EQUAL and their corresponding sides are PROPORTIONAL.
Question 2
Give two different examples of pair of
(i) Similar figures
(ii) Non-similar figures
(i) Similar figures
(ii) Non-similar figures
Solution 2
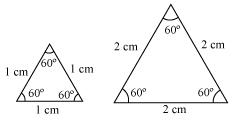
(i) Two equilateral triangles with sides 1 cm and 2 cm.
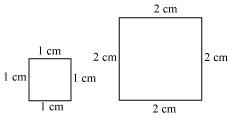
Two squares with sides 1 cm and 2 cm
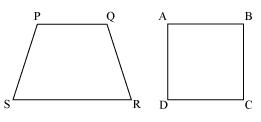
(ii) Trapezium and Square
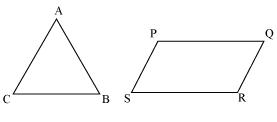
Triangle and Parallelogram

Two squares with sides 1 cm and 2 cm

(ii) Trapezium and Square

Triangle and Parallelogram

Question 3
State whether the following quadrilaterals are similar or not:
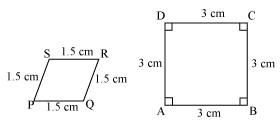

Solution 3
Quadrilateral PQRS and ABCD are not similar as their corresponding sides are proportional i.e. 1:2 but their corresponding angles are not equal.
NCERT Solution for Class 10 Mathematics Chapter 6 - Triangles Page/Excercise 6.2
Question 1
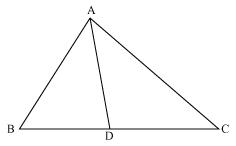
In figure. (i) and (ii) below, DE || BC. Find EC in (i) and AD in (ii).
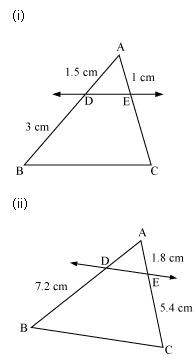

Solution 1
(i)

Let EC = x
Since DE || BC.
Therefore, by basic proportionality theorem,
 (ii)
(ii)
Let AD = x
Since DE || BC,
Therefore by basic proportionality theorem,


Let EC = x
Since DE || BC.
Therefore, by basic proportionality theorem,
 (ii)
(ii) 
Let AD = x
Since DE || BC,
Therefore by basic proportionality theorem,

Question 2
E and F are points on the sides PQ and PR respectively of a  PQR. For each of the following cases, state whether EF || QR.
PQR. For each of the following cases, state whether EF || QR.
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
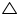 PQR. For each of the following cases, state whether EF || QR.
PQR. For each of the following cases, state whether EF || QR. (i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Solution 2
(i)
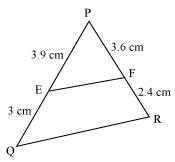
Given that PE = 3.9, EQ = 3, PF = 3.6, FR = 2.4
Now,

(ii)
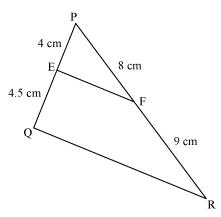
PE = 4, QE = 4.5, PF = 8, RF = 9

(iii)
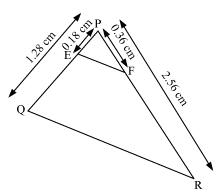
PQ = 1.28, PR = 2.56, PE = 0.18, PF = 0.36


Given that PE = 3.9, EQ = 3, PF = 3.6, FR = 2.4
Now,

(ii)

PE = 4, QE = 4.5, PF = 8, RF = 9

(iii)

PQ = 1.28, PR = 2.56, PE = 0.18, PF = 0.36

Question 3
In figure, if LM || CB and LN || CD, prove that


Solution 3
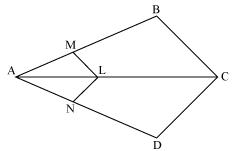
In the given figure
Since LM || CB,
Therefore by basic proportionality theorem,

Question 4
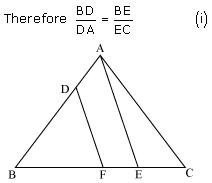
In figure , DE || AC and DF || AE. Prove that
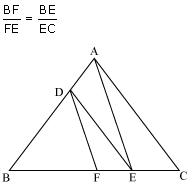

Solution 4
In
 ABC,
ABC,Since DE || AC

Question 5
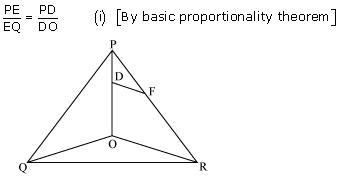
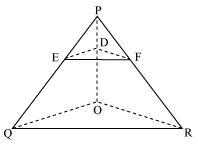
In figure , DE || OQ and DF || OR, show that EF || QR.


Solution 5
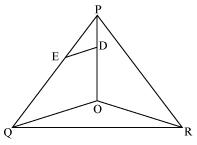
In
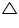 POQ
POQSince DE || OQ

Question 6


Solution 6
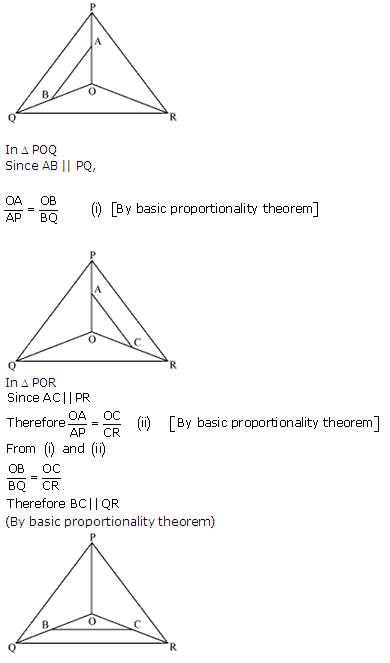
Question 7
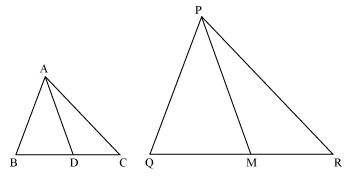
Using Basic proportionality Theorem, prove that a line drawn through the mid-points of one side of a triangle parallel to another side bisects the third side.
Solution 7

Consider the given figure
PQ is a line segment drawn through midpoint P of line AB such that PQ||BC
i.e. AP = PB
Now, by basic proportionality theorem

i.e. AQ = QC
Or, Q is midpoint of AC.
Question 8
Using converse of Basic Proportionality Theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
Solution 8
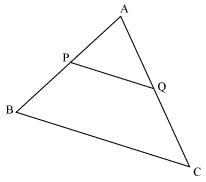
Consider the given figure
PQ is a line segment joining midpoints P and Q of line AB and AC respectively.
i.e. AP = PB and AQ = QC
Now, we may observe that
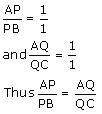
And hence basic proportionality theorem is verified
So, PQ||BC
Question 9
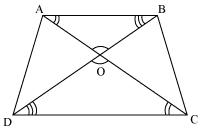
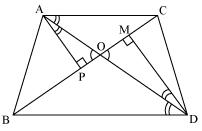
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that
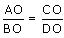
Solution 9

Question 10
The diagonals of a quadrilateral ABCD intersect each other at the point O such that 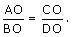 Show that ABCD is a trapezium.
Show that ABCD is a trapezium.
Solution 10
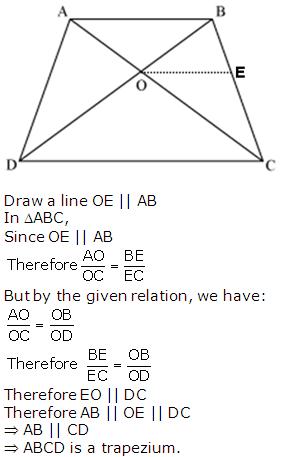
NCERT Solution for Class 10 Mathematics Chapter 6 - Triangles Page/Excercise 6.3
Question 1
State which pairs of triangles in figure are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
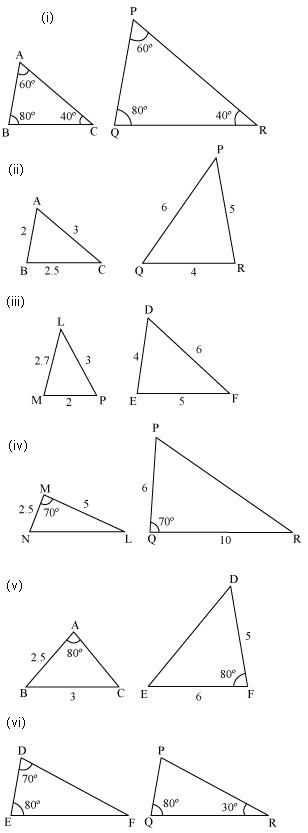

Solution 1
(i)  A =
A =  P = 60�
P = 60�
 B =
B =  Q = 80�
Q = 80�
 C =
C =  R = 40�
R = 40�
Therefore ABC ~
ABC ~  PQR [by AAA rule]
PQR [by AAA rule]

(iii) Triangles are not similar as the corresponding sides are not proportional.
(iv) Triangles are not similar as the corresponding sides are not proportional.
(v) Triangles are not similar as the corresponding sides are not proportional.
(vi) In DEF
DEF
 D +
D +  E +
E +  F = 180�
F = 180�
(Sum of measures of angles of a triangle is 180�)
70� + 80� + F = 180�
F = 180�
 F = 30�
F = 30�
Similarly in PQR
PQR
 P +
P +  Q +
Q +  R = 180�
R = 180�
(Sum of measures of angles of a triangle is 180�)
 P + 80� +30� = 180�
P + 80� +30� = 180�
 P = 70�
P = 70�
Now In DEF and
DEF and  PQR
PQR
 D =
D =  P = 70�
P = 70�
 E =
E =  Q = 80�
Q = 80�
 F =
F =  R = 30�
R = 30�
Therefore DEF ~
DEF ~  PQR [by AAA rule]
PQR [by AAA rule]
 A =
A =  P = 60�
P = 60� B =
B =  Q = 80�
Q = 80� C =
C =  R = 40�
R = 40�Therefore
 ABC ~
ABC ~  PQR [by AAA rule]
PQR [by AAA rule]
(iii) Triangles are not similar as the corresponding sides are not proportional.
(iv) Triangles are not similar as the corresponding sides are not proportional.
(v) Triangles are not similar as the corresponding sides are not proportional.
(vi) In
 DEF
DEF D +
D +  E +
E +  F = 180�
F = 180�(Sum of measures of angles of a triangle is 180�)
70� + 80� +
 F = 180�
F = 180� F = 30�
F = 30� Similarly in
 PQR
PQR P +
P +  Q +
Q +  R = 180�
R = 180�(Sum of measures of angles of a triangle is 180�)
 P + 80� +30� = 180�
P + 80� +30� = 180� P = 70�
P = 70� Now In
 DEF and
DEF and  PQR
PQR D =
D =  P = 70�
P = 70� E =
E =  Q = 80�
Q = 80� F =
F =  R = 30�
R = 30�Therefore
 DEF ~
DEF ~  PQR [by AAA rule]
PQR [by AAA rule]
Question 2
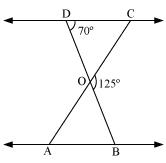
In figure ,  ODC ~
ODC ~  OBA,
OBA,  BOC = 125� and
BOC = 125� and  CDO = 70�. Find
CDO = 70�. Find  DOC,
DOC,  DCO and
DCO and  OAB
OAB
 ODC ~
ODC ~  OBA,
OBA,  BOC = 125� and
BOC = 125� and  CDO = 70�. Find
CDO = 70�. Find  DOC,
DOC,  DCO and
DCO and  OAB
OAB 
Solution 2
Since DOB is a straight line
Therefore DOC +
DOC +  COB = 180�
COB = 180�
Therefore DOC = 180� - 125�
DOC = 180� - 125�
= 55�
In DOC,
DOC,
 DCO +
DCO +  CDO +
CDO +  DOC = 180�
DOC = 180�
 DCO + 70� + 55� = 180�
DCO + 70� + 55� = 180�
 DCO = 55�
DCO = 55�
Since ODC ~
ODC ~ 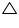 OBA,
OBA,
Therefore OCD =
OCD =  OAB [corresponding angles equal in similar triangles]
OAB [corresponding angles equal in similar triangles]
Therefore
 DOC +
DOC +  COB = 180�
COB = 180�Therefore
 DOC = 180� - 125�
DOC = 180� - 125�= 55�
In
 DOC,
DOC, DCO +
DCO +  CDO +
CDO +  DOC = 180�
DOC = 180� DCO + 70� + 55� = 180�
DCO + 70� + 55� = 180� DCO = 55�
DCO = 55�Since
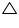 ODC ~
ODC ~ 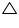 OBA,
OBA,Therefore
 OCD =
OCD =  OAB [corresponding angles equal in similar triangles]
OAB [corresponding angles equal in similar triangles]
Therefore  OAB = 55�
OAB = 55�
 OAB = 55�
OAB = 55�
Question 3
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that 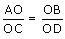
Solution 3
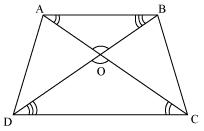
In
 DOC and
DOC and  BOA
BOAAB || CD
Therefore
 CDO =
CDO =  ABO [Alternate interior angles]
ABO [Alternate interior angles] DCO =
DCO =  BAO [Alternate interior angles]
BAO [Alternate interior angles] DOC =
DOC =  BOA [Vertically opposite angles]
BOA [Vertically opposite angles]Therefore
 DOC ~
DOC ~  BOA [AAA rule)
BOA [AAA rule)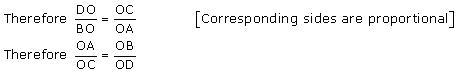
Question 4
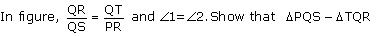
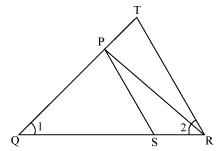

Solution 4
In  PQR
PQR
 PQR =
PQR = 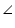 PRQ
PRQ
Therefore PQ = PR (i)
Given,

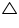 PQR
PQR 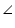 PQR =
PQR = 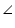 PRQ
PRQTherefore PQ = PR (i)
Given,

Question 5
S and T are point on sides PR and QR of  PQR such that
PQR such that  P =
P =  RTS. Show that
RTS. Show that  RPQ ~
RPQ ~  RTS.
RTS.
 PQR such that
PQR such that  P =
P =  RTS. Show that
RTS. Show that  RPQ ~
RPQ ~  RTS.
RTS.
Solution 5

In
 RPQ and
RPQ and  RST
RST RTS =
RTS =  QPS [given]
QPS [given] R =
R =  R [common angle]
R [common angle] RST =
RST =  RQP [ Remaining angles]
RQP [ Remaining angles]Therefore
 RPQ ~
RPQ ~  RTS [by AAA rule]
RTS [by AAA rule]
Question 6
In figure, If  ABE ~
ABE ~  ACD, show that
ACD, show that  ADE ~
ADE ~  ABC.
ABC.
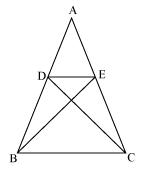
 ABE ~
ABE ~  ACD, show that
ACD, show that  ADE ~
ADE ~  ABC.
ABC. 
Solution 6
Since  ABE ~
ABE ~  ACD
ACD
Therefore AB = AC (1)
AD = AE (2)
Now, in ADE and
ADE and 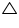 ABC,
ABC,
Dividing equation (2) by (1)
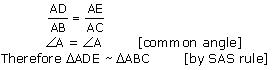
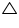 ABE ~
ABE ~ 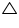 ACD
ACDTherefore AB = AC (1)
AD = AE (2)
Now, in
 ADE and
ADE and  ABC,
ABC,Dividing equation (2) by (1)
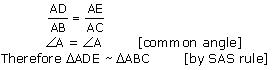
Question 7
In figure , altitudes AD and CE of  ABC intersect each other at the point P. Show that:
ABC intersect each other at the point P. Show that:

 ABC intersect each other at the point P. Show that:
ABC intersect each other at the point P. Show that: 
Solution 7
(i)
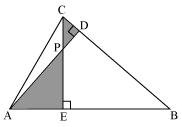
In AEP and
AEP and  CDP
CDP
Since CDP =
CDP =  AEP = 90�
AEP = 90�
 CPD =
CPD =  APE (vertically opposite angles)
APE (vertically opposite angles)
 PCD =
PCD =  PAE (remaining angle)
PAE (remaining angle)
Therefore by AAA rule,
 AEP ~
AEP ~  CDP
CDP
(ii)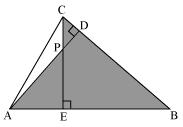
In ABD and
ABD and  CBE
CBE
 ADB =
ADB =  CEB = 90�
CEB = 90�
 ABD =
ABD =  CBE (common angle)
CBE (common angle)
 DAB =
DAB =  ECB (remaining angle)
ECB (remaining angle)
Therefore by AAA rule
 ABD ~
ABD ~  CBE
CBE
(iii)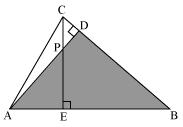
In AEP and
AEP and  ADB
ADB
 AEP =
AEP =  ADB = 90�
ADB = 90�
 PAE =
PAE =  DAB (common angle)
DAB (common angle)
 APE =
APE =  ABD (remaining angle)
ABD (remaining angle)
Therefore by AAA rule
 AEP ~
AEP ~  ADB
ADB
(iv)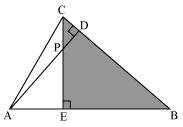
In PDC and
PDC and  BEC
BEC
 PDC =
PDC =  BEC = 90�
BEC = 90�
 PCD =
PCD =  BCE (common angle)
BCE (common angle)
 CPD =
CPD =  CBE
CBE
Therefore by AAA rule
 PDC ~
PDC ~  BEC
BEC

In
 AEP and
AEP and  CDP
CDPSince
 CDP =
CDP =  AEP = 90�
AEP = 90� CPD =
CPD =  APE (vertically opposite angles)
APE (vertically opposite angles) PCD =
PCD =  PAE (remaining angle)
PAE (remaining angle)Therefore by AAA rule,
 AEP ~
AEP ~  CDP
CDP (ii)

In
 ABD and
ABD and  CBE
CBE ADB =
ADB =  CEB = 90�
CEB = 90� ABD =
ABD =  CBE (common angle)
CBE (common angle) DAB =
DAB =  ECB (remaining angle)
ECB (remaining angle)Therefore by AAA rule
 ABD ~
ABD ~  CBE
CBE (iii)

In
 AEP and
AEP and  ADB
ADB AEP =
AEP =  ADB = 90�
ADB = 90� PAE =
PAE =  DAB (common angle)
DAB (common angle) APE =
APE =  ABD (remaining angle)
ABD (remaining angle)Therefore by AAA rule
 AEP ~
AEP ~  ADB
ADB (iv)

In
 PDC and
PDC and  BEC
BEC PDC =
PDC =  BEC = 90�
BEC = 90� PCD =
PCD =  BCE (common angle)
BCE (common angle) CPD =
CPD =  CBE
CBETherefore by AAA rule
 PDC ~
PDC ~  BEC
BEC
Question 8
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that  ABE ~
ABE ~  CFB
CFB
 ABE ~
ABE ~  CFB
CFB
Solution 8
 ABE and
ABE and  CFB
CFB A =
A =  C (opposite angles of a parallelogram)
C (opposite angles of a parallelogram) AEB =
AEB =  CBF (Alternate interior angles AE || BC)
CBF (Alternate interior angles AE || BC) ABE =
ABE =  CFB (remaining angle)
CFB (remaining angle)Therefore
 ABE ~
ABE ~  CFB (by AAA rule)
CFB (by AAA rule)
Question 9
In figure, ABC and AMP are two right triangles, right angled at B and M respectively, prove that:
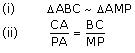

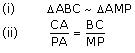
Solution 9
In 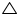 ABC and
ABC and  AMP
AMP
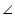 ABC =
ABC = 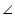 AMP = 90�
AMP = 90�
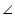 A =
A = 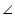 A (common angle)
A (common angle)
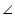 ACB =
ACB = 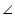 APM (remaining angle)
APM (remaining angle)
Therefore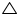 ABC ~
ABC ~ 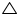 AMP (by AAA rule)
AMP (by AAA rule)
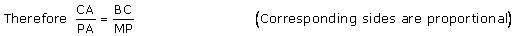
 ABC and
ABC and  AMP
AMP ABC =
ABC = 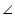 AMP = 90�
AMP = 90�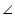 A =
A = 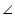 A (common angle)
A (common angle)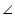 ACB =
ACB = 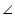 APM (remaining angle)
APM (remaining angle)Therefore
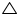 ABC ~
ABC ~ 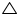 AMP (by AAA rule)
AMP (by AAA rule)
Question 10
CD and GH are respectively the bisectors of 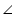 ACB and
ACB and  EGF such that D and H lie on sides AB and FE of
EGF such that D and H lie on sides AB and FE of  ABC and
ABC and  EFG respectively. If
EFG respectively. If  ABC ~
ABC ~ 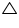 FEG, Show that:
FEG, Show that:

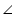 ACB and
ACB and 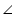 EGF such that D and H lie on sides AB and FE of
EGF such that D and H lie on sides AB and FE of 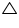 ABC and
ABC and  EFG respectively. If
EFG respectively. If  ABC ~
ABC ~  FEG, Show that:
FEG, Show that: 
Solution 10
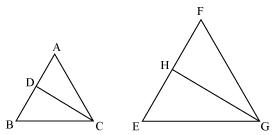
Since
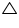 ABC ~
ABC ~ 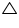 FEG
FEGTherefore
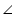 A =
A = 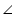 F
F  B =
B =  E
E As,
 ACB =
ACB =  FGE
FGETherefore
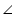 ACD =
ACD = 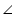 FGH (angle bisector)
FGH (angle bisector)And
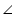 DCB =
DCB = 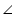 HGE (angle bisector)
HGE (angle bisector)Therefore
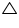 ACD ~
ACD ~ 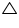 FGH (by AAA rule)
FGH (by AAA rule)And
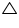 DCB ~
DCB ~ 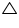 HGE (by AAA rule)
HGE (by AAA rule) 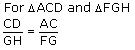
Question 11
In figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD  BC and EF
BC and EF  AC, prove that
AC, prove that  ABD ~
ABD ~  ECF
ECF
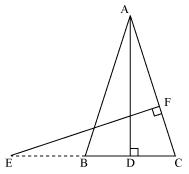
 ABD ~
ABD ~  ECF
ECF 
Solution 11
In  ABD and
ABD and  ECF,
ECF,
Given that AB = AC (isosceles triangles)
So,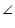 ABD =
ABD = 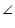 ECF
ECF
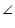 ADB =
ADB = 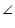 EFC = 90�
EFC = 90�
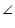 BAD =
BAD = 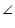 CEF
CEF
Therefore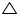 ABD ~
ABD ~ 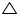 ECF (by AAA rule)
ECF (by AAA rule)
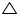 ABD and
ABD and 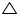 ECF,
ECF,Given that AB = AC (isosceles triangles)
So,
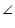 ABD =
ABD = 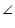 ECF
ECF 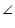 ADB =
ADB = 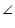 EFC = 90�
EFC = 90�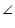 BAD =
BAD = 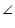 CEF
CEFTherefore
 ABD ~
ABD ~  ECF (by AAA rule)
ECF (by AAA rule)
Question 12
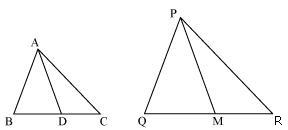
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of  PQR.
PQR.
Show that  ABC ~
ABC ~ 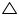 PQR.
PQR.
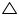 PQR.
PQR. Show that
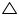 ABC ~
ABC ~ 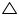 PQR.
PQR.
Solution 12
Median divides opposite side.
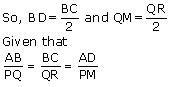
Therefore
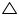 ABD ~
ABD ~  PQM (by SSS rule)
PQM (by SSS rule)Therefore
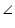 ABD =
ABD = 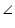 PQM (corresponding angles of similar triangles)
PQM (corresponding angles of similar triangles)Therefore
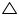 ABC ~
ABC ~ 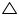 PQR (by SAS rule)
PQR (by SAS rule)
Question 13
D is a point on the side BC of a triangle ABC such that 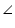 ADC =
ADC = 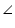 BAC. Show that
CA2 = CB.CD
BAC. Show that
CA2 = CB.CD
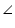 ADC =
ADC = 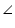 BAC. Show that
BAC. Show that
Solution 13
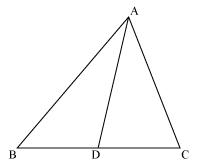
In
 ADC and
ADC and  BAC
BACGiven that
 ADC =
ADC = 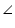 BAC
BAC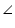 ACD =
ACD = 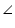 BCA (common angle)
BCA (common angle)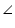 CAD =
CAD = 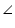 CBA (remaining angle)
CBA (remaining angle)Hence,
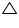 ADC ~
ADC ~ 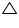 BAC [by AAA rule]
BAC [by AAA rule]So, corresponding sides of similar triangles will be proportional to each other
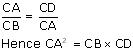
Question 14
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that
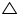 ABC ~
ABC ~ 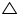 PQR
PQR
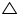 ABC ~
ABC ~ 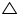 PQR
PQR
Solution 14

Question 15
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution 15
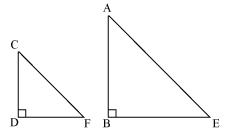
Let AB be a tower
CD be a pole
Shadow of AB is BE
Shadow of CD is DF
The light rays from sun will fall on tower and pole at same angle and at the same time.
So,
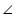 DCF =
DCF = 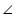 BAE
BAEAnd
 DFC =
DFC = 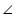 BEA
BEA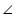 CDF =
CDF = 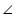 ABE (tower and pole are vertical to ground)
ABE (tower and pole are vertical to ground) Therefore
 ABE ~
ABE ~  CDF
CDF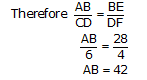
So, height of tower will be 42 meters.
Question 16
If AD and PM are medians of triangles ABC and PQR, respectively where  ABC ~
ABC ~ 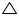 PQR prove that
PQR prove that
 ABC ~
ABC ~  PQR prove that
PQR prove that
Solution 16
Since
 ABC ~
ABC ~  PQR
PQRSo, their respective sides will be in proportion
Also,
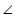 A =
A = 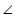 P,
P, 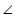 B =
B = 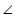 Q,
Q, 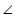 C =
C = 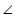 R (2)
R (2)Since, AD and PM are medians so they will divide their opposite sides in equal halves.
From equation (1) and (3)

So, we had observed that two respective sides are in same proportion in both triangles and also angle included between them is respectively equal
Hence,
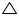 ABD ~
ABD ~ 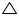 PQM (by SAS rule)
PQM (by SAS rule)NCERT Solution for Class 10 Mathematics Chapter 6 - Triangles Page/Excercise 6.4
Question 1
Let 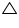 ABC ~
ABC ~ 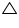 DEF their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
DEF their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
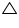 ABC ~
ABC ~ 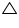 DEF their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
DEF their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
Solution 1

Question 2
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
Solution 2
Since AB || CD
 OAB =
OAB =  OCD (Alternate interior angles)
OCD (Alternate interior angles) OBA =
OBA = 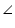 ODC (Alternate interior angles)
ODC (Alternate interior angles)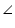 AOB =
AOB = 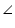 COD (Vertically opposite angles)
COD (Vertically opposite angles)Therefore
 AOB ~
AOB ~ 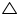 COD (By AAA rule)
COD (By AAA rule)
Question 3
In figure 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that 

Solution 3
Since
 ABC and
ABC and  DBC are one same base,
DBC are one same base,Therefore ratio between their areas will be as ratio of their heights.
Let us draw two perpendiculars AP and DM on line BC.
In
 APO and
APO and  DMO,
DMO, APO =
APO = 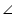 DMO = 90�
DMO = 90�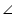 AOP =
AOP = 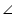 DOM (vertically opposite angles)
DOM (vertically opposite angles)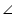 OAP =
OAP =  ODM (remaining angle)
ODM (remaining angle) Therefore
 APO ~
APO ~  DMO (By AAA rule)
DMO (By AAA rule)
Question 4
If the areas of two similar triangles are equal, prove that they are congruent.
Solution 4
Let us assume two similar triangles as  ABC ~
ABC ~  PQR
PQR

 ABC ~
ABC ~  PQR
PQR 
Question 5
D, E and F are respectively the mid-points of sides AB, BC and CA of  ABC. Find the ratio of the area of
ABC. Find the ratio of the area of  DEF and
DEF and  ABC.
ABC.
 ABC. Find the ratio of the area of
ABC. Find the ratio of the area of  DEF and
DEF and  ABC.
ABC.
Solution 5

Since D and E are mid points of
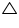 ABC
ABC
Question 6
Prove that the ratio of the areas of two similar triangles is equal to the square
of the ratio of their corresponding medians.
of the ratio of their corresponding medians.
Solution 6
Let us assume two similar triangles as
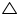 ABC ~
ABC ~  PQR. Let AD and PS be the medians of these triangles.
PQR. Let AD and PS be the medians of these triangles. 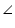 A =
A = 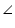 P,
P, 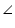 B =
B =  Q,
Q,  C =
C =  R
RSince, AD and PS are medians

Question 7
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution 7
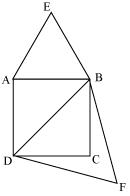
Let ABCD be a square of side a.
Therefore its diagonal
Two desired equilateral triangles are formed as
 ABE and
ABE and  DBF
DBFSide of an equilateral triangle
 ABE described on one of its side = a
ABE described on one of its side = aSide of an equilateral triangle
 DBF described on one of its diagonal
DBF described on one of its diagonal We know that equilateral triangles are having all its angles as 60º and all its sides of same length. So, all equilateral triangles are similar to each other. So, ratio between areas of these triangles will be equal to the square of the ratio between sides of these triangles.
Question 8
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
Solution 8
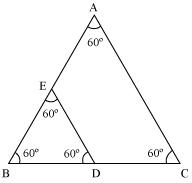
We know that equilateral triangles are having all its angles as 60º and all its sides of same length. So, all equilateral triangles are similar to each other. So, ratio between areas of these triangles will be equal to the square of the ratio between sides of these triangles.
Let side of
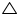 ABC = x
ABC = x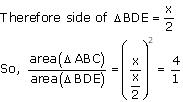 Hence, (c)
Hence, (c)
Question 9
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
Solution 9
If, two triangles are similar to each other, ratio between areas of these triangles will be equal to the square of the ratio between sides of these triangles.
Given that sides are in the ratio 4:9.
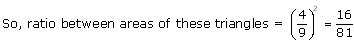
Hence, (d).
Given that sides are in the ratio 4:9.
Hence, (d).
NCERT Solution for Class 10 Mathematics Chapter 6 - Triangles Page/Excercise 6.5
Question 1
Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
Solution 1
i.Given that sides are 7 cm, 24 cm, and 25 cm. Squaring the lengths of these sides we get 49, 576, and 625.
Clearly, 49 + 576 = 625 or 72 + 242 = 252 .
Therefore, given triangle is satisfying Pythagoras theorem. So, it is a right triangle. The longest side in a right angled triangle is the hypotenuse.
Therefore length of hypotenuse of this triangle = 25 cm.
ii.Given that sides are 3 cm, 8 cm, and 6 cm. Squaring the lengths of these sides we may get 9, 64, and 36. Clearly, sum of squares of lengths of two sides is not equal to square of length of third side. Therefore given triangle is not satisfying Pythagoras theorem. So, it is not a right triangle
iii.Given that sides are 50 cm, 80 cm, and 100 cm. Squaring the lengths of these sides we may get 2500, 6400, and 10000. Clearly, sum of squares of lengths of two sides is not equal to square of length of third side. Therefore given triangle is not satisfying Pythagoras theorem. So, it is not a right triangle.
iv.Given that sides are 13 cm, 12 cm, and 5 cm. Squaring the lengths of these sides we may get 169, 144, and 25. Clearly, 144 +25 = 169 Or, 122 + 52 = 132.
ii.Given that sides are 3 cm, 8 cm, and 6 cm. Squaring the lengths of these sides we may get 9, 64, and 36. Clearly, sum of squares of lengths of two sides is not equal to square of length of third side. Therefore given triangle is not satisfying Pythagoras theorem. So, it is not a right triangle
iii.Given that sides are 50 cm, 80 cm, and 100 cm. Squaring the lengths of these sides we may get 2500, 6400, and 10000. Clearly, sum of squares of lengths of two sides is not equal to square of length of third side. Therefore given triangle is not satisfying Pythagoras theorem. So, it is not a right triangle.
iv.Given that sides are 13 cm, 12 cm, and 5 cm. Squaring the lengths of these sides we may get 169, 144, and 25. Clearly, 144 +25 = 169 Or, 122 + 52 = 132.
Therefore given triangle is satisfying Pythagoras theorem. So, it is a right triangle.
The longest side in a right angled triangle is the hypotenuse.
Therefore length of hypotenuse of this triangle = 13 cm.
The longest side in a right angled triangle is the hypotenuse.
Therefore length of hypotenuse of this triangle = 13 cm.
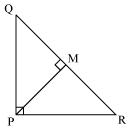
Question 2
PQR is a triangle right angled at P and M is a point on QR such that PM  QR. Show that PM2 = QM x MR.
QR. Show that PM2 = QM x MR.
 QR. Show that PM2 = QM x MR.
QR. Show that PM2 = QM x MR.
Solution 2

Question 3
In figure 6.53, ABD is a triangle right angled at A and AC  BD. Show that
BD. Show that
(i) AB2 = BC x BD
(ii) AC2 = BC x DC
(iii) AD2 = BD x CD
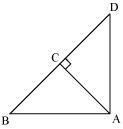
(i) AB2 = BC x BD
(ii) AC2 = BC x DC
(iii) AD2 = BD x CD

Solution 3


iii. In
 DCA &
DCA &  DAB
DAB  DCA =
DCA =  DAB = 90º
DAB = 90º CDA =
CDA =  ADB (common angle)
ADB (common angle) DAC =
DAC =  DBA (remaining angle)
DBA (remaining angle)
Question 4
ABC is an isosceles triangle right angled at C. prove that AB2 = 2 AC2.
Solution 4
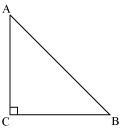
Given that
 ABC is an isosceles triangle.
ABC is an isosceles triangle.Therefore AC = CB
Applying Pythagoras theorem in ABC (i.e. right angled at point C)
Question 5
ABC is an isosceles triangle with AC = BC. If AB2 = 2 AC2, prove that ABC is a right triangle.
Solution 5
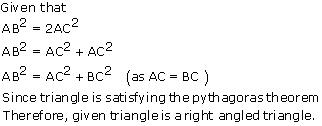
Question 6
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Solution 6
Let AD be the altitude in given equilateral triangle
 ABC.
ABC. We know that altitude bisects the opposite side.
So, BD = DC = a

Since in an equilateral triangle, all the altitudes are equal in length.
So, length of each altitude will be
Question 7
Prove that the sum of the squares of the sides of rhombus is equal to the sum of the squares of its diagonals.
Solution 7
In
 AOB,
AOB,  BOC,
BOC,  COD,
COD, 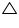 AOD
AODApplying Pythagoras theorem
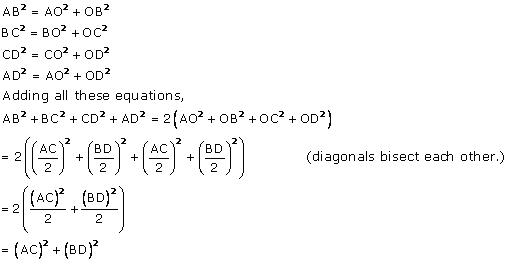
Question 8
In figure 6.54, O is a point in the interior of a triangle ABC, OD  BC, OE
BC, OE  AC and OF
AC and OF  AB. Show that
AB. Show that
(i) OA2 + OB2 + OC2 - OD2 - OE2 - OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2

(i) OA2 + OB2 + OC2 - OD2 - OE2 - OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
Solution 8


Question 9
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
Solution 9

Question 10
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Solution 10
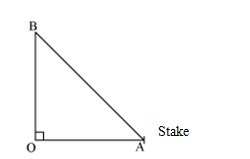
Let OB be the pole and AB be the wire.
Therefore by Pythagoras theorem,
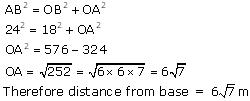
Question 11
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after 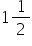 hours?
hours?
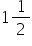 hours?
hours?
Solution 11
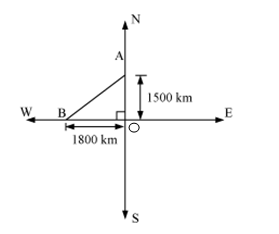

Let these distances are represented by OA and OB respectively.
Now applying Pythagoras theorem
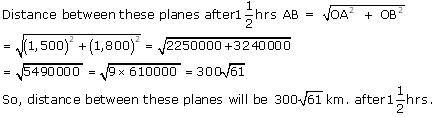
Question 12
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Solution 12
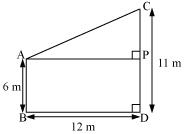
Let CD and AB be the poles of height 11 and 6 m.
Therefore CP = 11 - 6 = 5 m
From the figure we may observe that AP = 12m
In
 APC, by applying Pythagoras theorem
APC, by applying Pythagoras theorem 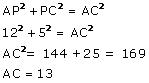
Therefore distance between their tops = 13 m.
Question 13
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
Solution 13

In
 ACE,
ACE, 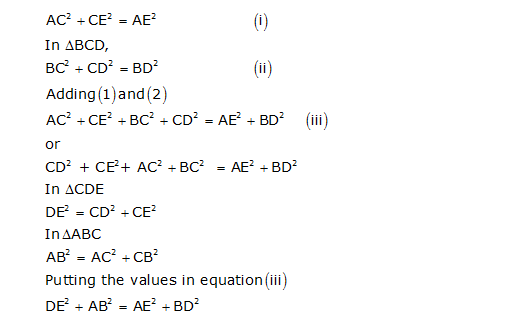
Question 14
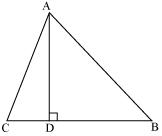
The perpendicular from A on side BC of a ABC intersect BC at D such that DB = 3 CD
Prove that 2 AB2 = 2 AC2 + BC2

Solution 14

Question 15
In an equilateral triangle ABC, D is a point on side BC such that BD = 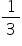 BC . Prove that 9 AD2 = 7 AB2
BC . Prove that 9 AD2 = 7 AB2
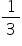 BC . Prove that 9 AD2 = 7 AB2
BC . Prove that 9 AD2 = 7 AB2
Solution 15
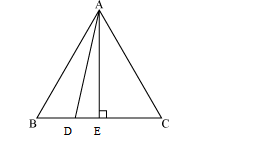

Question 16
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution 16

Let side of equilateral triangle be a. And AE be the altitude of
 ABC
ABC 
Now, in
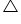 ABE by applying Pythagoras theorem
ABE by applying Pythagoras theorem AB2 = AE2 + BE2
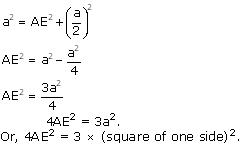
Question 17
Tick the correct answer and justify: In 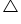 ABC, AB =
ABC, AB = 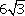 cm, AC = 12 cm and BC = 6 cm.
cm, AC = 12 cm and BC = 6 cm.
The angle B is:
 ABC, AB =
ABC, AB = The angle B is:
Solution 17
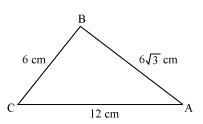
Given that AB =
We may observe that
AB2 = 108
AC2 = 144
And BC2 = 36
AB2 +BC2 = AC2
Thus the given triangle
 ABC is satisfying Pythagoras theorem
ABC is satisfying Pythagoras theorem Therefore triangle is a right angled triangle right angled at B
Therefore
 B = 90°.
B = 90°.Hence, (c).
NCERT Solution for Class 10 Mathematics Chapter 6 - Triangles Page/Excercise 6.6
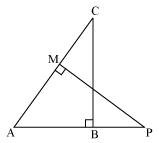
Question 1
In the given figure, PS is the bisector of  QPR of
QPR of  PQR. Prove that
PQR. Prove that

 QPR of
QPR of  PQR. Prove that
PQR. Prove that 
Solution 1
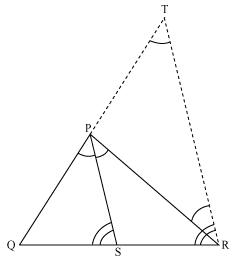
Let us draw a line segment RT parallel to SP which intersects extended line segment QP at point T.
Given that PS is angle bisector of
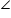 QPR.
QPR.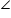 QPS =
QPS = 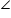 SPR (1)
SPR (1)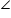 SPR =
SPR = 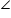 PRT (As PS || TR) (2)
PRT (As PS || TR) (2)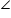 QPS =
QPS = 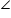 QTR (As PS || TR) (3)
QTR (As PS || TR) (3)Using these equations we may find
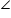 PRT =
PRT = 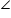 QTR from (2) and (3)
QTR from (2) and (3)So, PT = PR (Since
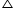 PTR is isosceles triangle)
PTR is isosceles triangle)Now in
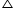 QPS and
QPS and 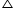 QTR
QTR QSP =
QSP =  QRT (As PS || TR)
QRT (As PS || TR) QPS =
QPS =  QTR (As PS || TR)
QTR (As PS || TR) Q is common
Q is common QPS ~
QPS ~  QTR
QTR
Question 2
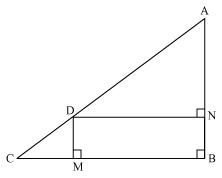
In the given figure, D is a point on hypotenuse AC of  ABC, DM
ABC, DM  BC and DN
BC and DN  AB, Prove that:
AB, Prove that:
(i). DM2 = DN.MC (ii). DN2 = DM.AN
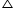 ABC, DM
ABC, DM (i). DM2 = DN.MC (ii). DN2 = DM.AN

Solution 2
(i). Let us join DB.
DN || CB
DM || AB
So, DN = MB
DM = NB
The condition to be proved is the case when DNBM is a square or D is the midpoint of side AC.
Then CDB =
CDB =  ADB = 90°
ADB = 90°
 2 +
2 +  3 = 90° (1)
3 = 90° (1)
In CDM
CDM
 1 +
1 +  2 +
2 +  DMC = 180°
DMC = 180°
 1 +
1 +  2 = 90° (2)
2 = 90° (2)
In DMB
DMB
 3 +
3 +  DMB +
DMB +  4 = 180°
4 = 180°
 3 +
3 +  4 = 90° (3)
4 = 90° (3)
From equation (1) and (2)
 1 =
1 =  3
3
From equation (1) and (3)
 2 =
2 =  4
4
 BDM ~
BDM ~  DCM
DCM

(ii). Similarly in DBN
DBN
 4 +
4 +  3 = 90° (4)
3 = 90° (4)
In DAN
DAN
 5 +
5 +  6 = 90° (5)
6 = 90° (5)
In DAB
DAB
 4 +
4 +  5 = 90° (6)
5 = 90° (6)
From equation (4) and (6)
 3 =
3 =  5
5
From equation (5) and (6)
 4 =
4 =  6
6
 DNA ~
DNA ~  BND
BND


DN || CB
DM || AB
So, DN = MB
DM = NB
The condition to be proved is the case when DNBM is a square or D is the midpoint of side AC.
Then
 CDB =
CDB =  ADB = 90°
ADB = 90° 2 +
2 +  3 = 90° (1)
3 = 90° (1)In
 CDM
CDM 1 +
1 +  2 +
2 +  DMC = 180°
DMC = 180° 1 +
1 +  2 = 90° (2)
2 = 90° (2)In
 DMB
DMB 3 +
3 +  DMB +
DMB +  4 = 180°
4 = 180° 3 +
3 +  4 = 90° (3)
4 = 90° (3)From equation (1) and (2)
 1 =
1 =  3
3From equation (1) and (3)
 2 =
2 =  4
4 BDM ~
BDM ~  DCM
DCM
(ii). Similarly in
 DBN
DBN 4 +
4 +  3 = 90° (4)
3 = 90° (4)In
 DAN
DAN 5 +
5 +  6 = 90° (5)
6 = 90° (5)In
 DAB
DAB 4 +
4 +  5 = 90° (6)
5 = 90° (6)From equation (4) and (6)
 3 =
3 =  5
5From equation (5) and (6)
 4 =
4 =  6
6 DNA ~
DNA ~  BND
BND
Question 3
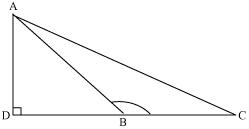
In the given figure, ABC is a triangle in which  ABC> 90° and AD
ABC> 90° and AD  CB produced.
Prove that AC2 = AB2 + BC2 + 2BC . BD.
CB produced.
Prove that AC2 = AB2 + BC2 + 2BC . BD.
 ABC> 90° and AD
ABC> 90° and AD 
Solution 3
In  ADB applying Pythagoras theorem
ADB applying Pythagoras theorem
AB2 = AD2 + DB2 (1)
In ACD applying Pythagoras theorem
ACD applying Pythagoras theorem
AC2 = AD2 + DC2
AC2 = AD2 + (DB + BC)2
AC2 = AD2 + DB2 + BC2 + 2DB x BC
Now using equation (1)
AC2 = AB2 + BC2 + 2BC . BD
 ADB applying Pythagoras theorem
ADB applying Pythagoras theoremAB2 = AD2 + DB2 (1)
In
 ACD applying Pythagoras theorem
ACD applying Pythagoras theoremAC2 = AD2 + DC2
AC2 = AD2 + (DB + BC)2
AC2 = AD2 + DB2 + BC2 + 2DB x BC
Now using equation (1)
AC2 = AB2 + BC2 + 2BC . BD
Question 4
In the given figure, ABC is a triangle in which 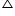 ABC < 90° and AD
ABC < 90° and AD  BC. Prove that AC2 = AB2 + BC2 - 2BC.BD.
BC. Prove that AC2 = AB2 + BC2 - 2BC.BD.
 ABC < 90° and AD
ABC < 90° and AD 
Solution 4
In  ADB applying Pythagoras theorem
ADB applying Pythagoras theorem
AD2 + DB2 = AB2
AD2 = AB2 - DB2 (1)
In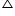 ADC applying Pythagoras theorem
ADC applying Pythagoras theorem
AD2 + DC2 = AC2 (2)
Now using equation (1)
AB2 - BD2 + DC2 = AC2
AB2 - BD2 + (BC - BD)2 = AC2
AC2 = AB2 - BD2 + BC2 + BD2 - 2BC. BD
= AB2 + BC2 - 2BC. BD
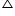 ADB applying Pythagoras theorem
ADB applying Pythagoras theoremAD2 + DB2 = AB2
AD2 = AB2 - DB2 (1)
In
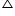 ADC applying Pythagoras theorem
ADC applying Pythagoras theoremAD2 + DC2 = AC2 (2)
Now using equation (1)
AB2 - BD2 + DC2 = AC2
AB2 - BD2 + (BC - BD)2 = AC2
AC2 = AB2 - BD2 + BC2 + BD2 - 2BC. BD
= AB2 + BC2 - 2BC. BD
Question 5
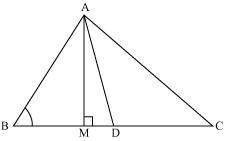
In the given figure, AD is a median of a triangle ABC and AM  BC. Prove that:
BC. Prove that:
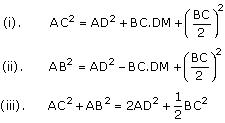

Solution 5
(i). In 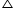 AMD
AMD
AM2 + MD2 = AD2 (1)
In AMC
AMC
AM2 + MC2 = AC2 (2)
AM2 + (MD + DC)2 = AC2
(AM2 + MD2) + DC2 + 2MD.DC = AC2
Using equation (1) we may get
AD2 + DC2 + 2MD.DC = AC2
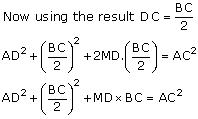
(ii). In ABM applying Pythagoras theorem
ABM applying Pythagoras theorem
AB2 = AM2 + MB2
= (AD2 - DM2) + MB2
= (AD2 - DM2) + (BD - MD)2
= AD2 - DM2 + BD2 + MD2 - 2BD.MD
= AD2 + BD2 - 2BD.MD
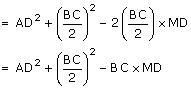
(iii). In AMB
AMB
AM2 + MB2 = AB2 (1)
In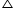 AMC
AMC
AM2 + MC2 = AC2 (2)
Adding equation (1) and (2)
2AM2 + MB2 + MC2 = AB2 + AC2
2AM2 + (BD - DM)2 + (MD + DC)2 = AB2 + AC2
2AM2+BD2 + DM2 - 2BD.DM + MD2 + DC2 + 2MD.DC = AB2 + AC2
2AM2 + 2MD2 + BD2 + DC2 + 2MD (-BD + DC) = AB2 + AC2
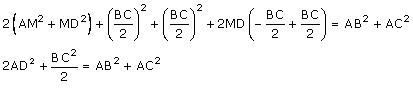
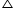 AMD
AMDAM2 + MD2 = AD2 (1)
In
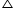 AMC
AMCAM2 + MC2 = AC2 (2)
AM2 + (MD + DC)2 = AC2
(AM2 + MD2) + DC2 + 2MD.DC = AC2
Using equation (1) we may get
AD2 + DC2 + 2MD.DC = AC2
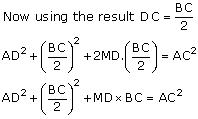
(ii). In
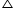 ABM applying Pythagoras theorem
ABM applying Pythagoras theoremAB2 = AM2 + MB2
= (AD2 - DM2) + MB2
= (AD2 - DM2) + (BD - MD)2
= AD2 - DM2 + BD2 + MD2 - 2BD.MD
= AD2 + BD2 - 2BD.MD
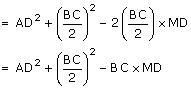
(iii). In
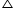 AMB
AMBAM2 + MB2 = AB2 (1)
In
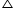 AMC
AMC AM2 + MC2 = AC2 (2)
Adding equation (1) and (2)
2AM2 + MB2 + MC2 = AB2 + AC2
2AM2 + (BD - DM)2 + (MD + DC)2 = AB2 + AC2
2AM2+BD2 + DM2 - 2BD.DM + MD2 + DC2 + 2MD.DC = AB2 + AC2
2AM2 + 2MD2 + BD2 + DC2 + 2MD (-BD + DC) = AB2 + AC2
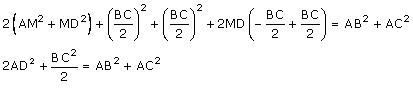
Question 6
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Solution 6
Let
 ABCD be a parallelogram
ABCD be a parallelogram Let us draw perpendicular DE on extended side AB and AF on side DC.
In
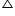 DEA
DEADE2 + EA2 = DA2 (i)
In
 DEB
DEBDE2 + EB2 = DB2
DE2 + (EA + AB)2 = DB2
(DE2 + EA2) + AB2 + 2EA. AB = DB2
DA2 + AB2 + 2EA.AB = DB2 (ii)
In
 ADF
ADFAD2 = AF2 + FD2
In
 AFC
AFCAC2 = AF2 + FC2
= AF2 + (DC - FD)2
= AF2 + DC2 + FD2 - 2DC - FD
= (AF2 + FD2) + DC2 - 2DC . FD
AC2 = AD2 + DC2 - 2DC FD (iii)
Since ABCD is a parallelogram
AB = CD (iii)
And BC = AD (iv)
In
 DEA and
DEA and 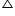 ADF
ADF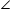 DEA =
DEA =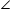 AFD
AFD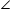 EAD =
EAD = 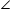 FDA (EA || DF)
FDA (EA || DF) EDA =
EDA =  FAD (AF || ED)
FAD (AF || ED)AD is common in both triangles.
Since respective angles are same and respective sides are same
 DEA
DEA 
 AFD
AFDSo EA = DF (v)
Adding equation (ii) and (iii)
DA2 + AB2 + 2EA.AB + AD2 + DC2 - 2DC.FD = DB2 + AC2
DA2 + AB2 + AD2 + DC2 + 2EA.AB - 2DC.FD = DB2 + AC2
BC2 + AB2 + AD2 + DC2 + 2EA.AB-2AB.EA = DB2 + AC2
AB2 + BC2 + CD2 + DA2 = AC2 + BD2
Question 7
In the given figure, two chords AB and CD intersect each other at the point P. prove that:
(i)  APC ~
APC ~  DPB (ii) AP.PB = CP.DP
DPB (ii) AP.PB = CP.DP
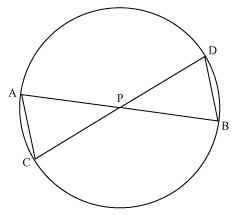
(i)
 APC ~
APC ~  DPB (ii) AP.PB = CP.DP
DPB (ii) AP.PB = CP.DP
Solution 7
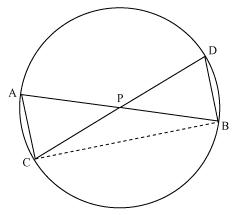
Let us join CB
(i) In
 APC and
APC and  DPB
DPB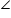 APC =
APC = 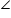 DPB {Vertically opposite angles}
DPB {Vertically opposite angles}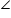 CAP =
CAP = 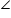 BDP {Angles in same segment for chord CB}
BDP {Angles in same segment for chord CB} APC ~
APC ~  DPB {BY AA similarly criterion}
DPB {BY AA similarly criterion}(ii) We know that corresponding sides of similar triangles are proportional
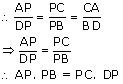
Question 8
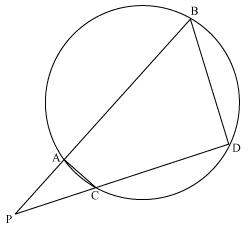
In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i)  PAC ~
PAC ~  PDB (ii) PA.PB = PC.PD
PDB (ii) PA.PB = PC.PD
(i)
 PAC ~
PAC ~  PDB (ii) PA.PB = PC.PD
PDB (ii) PA.PB = PC.PD
Solution 8
(i) In  PAC and
PAC and  PDB
PDB
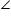 P =
P = 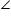 P (common)
P (common)
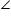 PAC =
PAC = 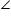 PDB (exterior angle of a cyclic quadrilateral is equal to opposite interior angle)
PDB (exterior angle of a cyclic quadrilateral is equal to opposite interior angle)
 PAC and
PAC and  PDB
PDB P =
P =  P (common)
P (common)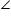 PAC =
PAC = 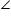 PDB (exterior angle of a cyclic quadrilateral is equal to opposite interior angle)
PDB (exterior angle of a cyclic quadrilateral is equal to opposite interior angle)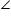 PCA =
PCA = 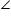 PBD
PBD PAC ~
PAC ~  PDB
PDB(ii) We know that corresponding sides of similar triangles are proportional.
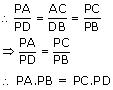
Question 9
in the given figure, D is a point on side BC of  ABC such that
ABC such that  .
Prove that AD is the bisector of
.
Prove that AD is the bisector of  BAC.
BAC.
 ABC such that
ABC such that  .
. BAC.
BAC. 
Solution 9
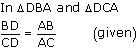
AD = AD (common)
So,
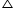 DBA ~
DBA ~ 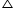 DCA (By SSS)
DCA (By SSS)Now, corresponding angles of similar triangles will be equal.
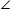 BAD =
BAD =  CAD
CADAD is angle bisector of
 BAC
BAC
Question 10
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see Fig. If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?
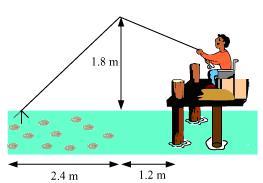

Solution 10
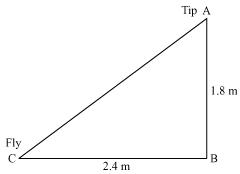
Let AB be the height of tip of fishing rod from water surface. Let BC be the horizontal distance of fly from the tip of fishing rod.
Then, AC is the length of string.
AC can be found by applying Pythagoras theorem in
 ABC
ABCAC2 = AB2 + BC2
AC2 = (1.8)2 + (2.4)2
AC2 = 3.24 + 5.76
AC2 = 9.00
AC = 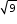 = 3
= 3
Thus, length of string out is 3 m. 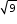 = 3
= 3Now, she pulls string at rate of 5 cm per second.
So, string pulled in 12 seconds = 12 x 5 = 60 cm = 0.6 m

Let after 12 second Fly be at point D.
Length of string out after 12 second is AD
AD = AC - string pulled by Nazima in 12 seconds
= 3.00 - 0.6
= 2.4
In
 ADB
ADBAB2 + BD2 = AD2
(1.8)2 + BD2 = (2.4)2
BD2 = 5.76 - 3.24 = 2.52
BD = 1.587
Horizontal distance of fly = BD + 1.2
= 1.587 + 1.2
= 2.787
= 2.79 m
No comments:
Post a Comment