NCERT Solution for Class 9 Mathematics Chapter 13 - Surface Areas and Volumes Page/Excercise 13.1
Question 1
A plastic box 1.5 m long, 1.25 m wide and 65 cm deep, is to be made. It is to be open at the top. Ignoring the thickness of the plastic sheet, determine:
(i) The area of the sheet required for making the box.
(ii) The cost of sheet for it, if a sheet measuring 1 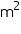 costs Rs 20.
A plastic box 1.5 m long, 1.25 m wide and 65 cm deep, is to be made. It is to be open at the top. Ignoring the thickness of the plastic sheet, determine:
(i) The area of the sheet required for making the box.
(ii) The cost of sheet for it, if a sheet measuring 1 m2 costs Rs 20.
costs Rs 20.
A plastic box 1.5 m long, 1.25 m wide and 65 cm deep, is to be made. It is to be open at the top. Ignoring the thickness of the plastic sheet, determine:
(i) The area of the sheet required for making the box.
(ii) The cost of sheet for it, if a sheet measuring 1 m2 costs Rs 20.
(i) The area of the sheet required for making the box.
(ii) The cost of sheet for it, if a sheet measuring 1
 costs Rs 20.
costs Rs 20.
Solution 1
Length of box = 1.5 m
Breadth of box = 1.25 m
Depth of box = 65 cm = 0.65 m
(i) The box is open at the top.
Area of sheet required = 2bh + 2lh + lb
= [2 1.25
1.25  0.65 + 2
0.65 + 2  1.5
1.5  0.65 + 1.5
0.65 + 1.5  1.25] m2
1.25] m2
= (1.625 + 1.95 + 1.875)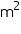 = 5.45
= 5.45 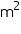
(ii) Cost of sheet of area 1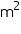 = Rs 20 Cost of sheet of area 5.45
= Rs 20 Cost of sheet of area 5.45 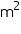 = Rs (5.45
= Rs (5.45  20) = Rs 109
20) = Rs 109
Breadth of box = 1.25 m
Depth of box = 65 cm = 0.65 m
(i) The box is open at the top.
Area of sheet required = 2bh + 2lh + lb
= [2
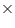 1.25
1.25 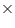 0.65 + 2
0.65 + 2 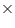 1.5
1.5 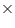 0.65 + 1.5
0.65 + 1.5 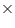 1.25] m2
1.25] m2= (1.625 + 1.95 + 1.875)
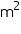 = 5.45
= 5.45 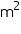
(ii) Cost of sheet of area 1
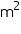 = Rs 20 Cost of sheet of area 5.45
= Rs 20 Cost of sheet of area 5.45 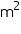 = Rs (5.45
= Rs (5.45 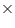 20) = Rs 109
20) = Rs 109
Question 2
The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of Rs 7.50 per 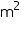 .
.
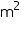 .
.
Solution 2
Length of room = 5 m
Breadth of room = 4 m
Height of room = 3 m
Area to be white washed = Area of walls + Area of ceiling of room
= 2lh + 2bh + lb
= [2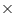 5
5 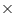 3 + 2
3 + 2 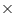 4
4 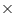 3 + 5
3 + 5 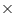 4]
4] 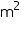
= (30 + 24 + 20)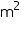
= 74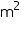
Cost of white washing 1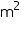 area = Rs 7.50
area = Rs 7.50
Cost of white washing 74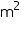 area = Rs (74
area = Rs (74  7.50) = Rs 555
7.50) = Rs 555
Breadth of room = 4 m
Height of room = 3 m
Area to be white washed = Area of walls + Area of ceiling of room
= 2lh + 2bh + lb
= [2
 5
5  3 + 2
3 + 2  4
4  3 + 5
3 + 5  4]
4] 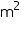
= (30 + 24 + 20)
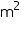
= 74
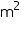
Cost of white washing 1
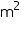 area = Rs 7.50
area = Rs 7.50Cost of white washing 74
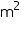 area = Rs (74
area = Rs (74 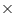 7.50) = Rs 555
7.50) = Rs 555
Question 3
The floor of a rectangular hall has a perimeter 250 m. If the cost of panting the four walls at the rate of Rs 10 per 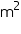 is Rs 15000, find the height of the hall.
is Rs 15000, find the height of the hall.
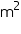 is Rs 15000, find the height of the hall.
is Rs 15000, find the height of the hall.
Solution 3
Let length, breadth and height of rectangular hall be l, b and h respectively.
Area of four walls = 2lh + 2bh = 2(l + b) h
Perimeter of floor of hall = 2(l + b) = 250 m
 Area of four walls = 2(l + b) h = 250h
Area of four walls = 2(l + b) h = 250h 
Cost of painting 1 area = Rs 10
area = Rs 10
Cost of painting 250h area = Rs (250h
area = Rs (250h  10) = Rs 2500h
10) = Rs 2500h
It is given that the cost of paining the walls is Rs 15000.
 15000 = 2500h
15000 = 2500h
h = 6
Thus, the height of hall is 6 m.
Area of four walls = 2lh + 2bh = 2(l + b) h
Perimeter of floor of hall = 2(l + b) = 250 m
Cost of painting 1
 area = Rs 10
area = Rs 10Cost of painting 250h
 area = Rs (250h
area = Rs (250h  10) = Rs 2500h
10) = Rs 2500hIt is given that the cost of paining the walls is Rs 15000.
h = 6
Thus, the height of hall is 6 m.
Question 4
The paint in a certain container is sufficient to paint an area equal to 9.375 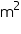 . How many bricks of dimensions 22.5 cm
. How many bricks of dimensions 22.5 cm 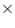 10 cm
10 cm 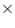 7.5 cm can be painted out of this container?
7.5 cm can be painted out of this container?
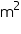 . How many bricks of dimensions 22.5 cm
. How many bricks of dimensions 22.5 cm  10 cm
10 cm  7.5 cm can be painted out of this container?
7.5 cm can be painted out of this container?
Solution 4
Total surface area of one brick = 2(lb + bh + lh)
= [2(22.5 10 + 10
10 + 10  7.5 + 22.5
7.5 + 22.5 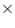 7.5)]
7.5)]
= 2(225 + 75 + 168.75)
= (2 468.75)
468.75) 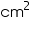
= 937.5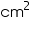
Let n number of bricks be painted by the container.
Area of n bricks = 937.5n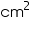
Area that can be painted by the container = 9.375 m2 = 93750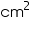
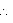 93750 = 937.5n
93750 = 937.5n
n = 100
Thus, 100 bricks can be painted out by the container.
= [2(22.5
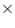 10 + 10
10 + 10 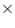 7.5 + 22.5
7.5 + 22.5 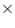 7.5)]
7.5)]
= 2(225 + 75 + 168.75)
= (2
 468.75)
468.75) 
= 937.5
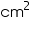
Let n number of bricks be painted by the container.
Area of n bricks = 937.5n
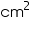
Area that can be painted by the container = 9.375 m2 = 93750
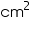
n = 100
Thus, 100 bricks can be painted out by the container.
Question 5
A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.
(i) Which box has the greater lateral surface area and by how much?
(ii) Which box has the smaller total surface area and by how much?
(i) Which box has the greater lateral surface area and by how much?
(ii) Which box has the smaller total surface area and by how much?
Solution 5
Edge of the cubical box = 10 cm
Length of the cuboidal box = 12.5 cm
Breadth of the cuboidal box = 10 cm
Height of the cuboidal box = 8 cm
Lateral surface area of cubical box = =
= 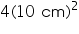 =
= 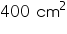
Lateral surface area of cuboidal box = 2[lh + bh]
= [2(12.5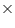 8 + 10
8 + 10 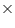 8)]
8)] 
= 360
The lateral surface area of cubical box is greater than lateral surface area of cuboidal box.
Lateral surface area of cubical box - lateral surface area of cuboidal box = 400 - 360
- 360  = 40
= 40 
Thus, the lateral surface area of cubical box is greater than that of cuboidal box by 40 cm2.
(ii) Total surface area of cubical box = =
=  = 600 cm2
= 600 cm2
Total surface area of cuboidal box = 2[lh + bh + lb]
= [2(12.5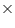 8 + 10
8 + 10 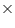 8 + 12.5
8 + 12.5 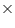 10]
10]  =
= 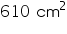
The total surface area of cubical box is smaller than that of cuboidal box
Total surface area of cuboidal box - total surface area of cubical box =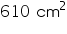 -
- 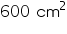 =
=
Thus, the total surface area of cubical box is smaller than that of cuboidal box by
Length of the cuboidal box = 12.5 cm
Breadth of the cuboidal box = 10 cm
Height of the cuboidal box = 8 cm
Lateral surface area of cubical box =
 =
= 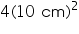 =
= 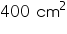
Lateral surface area of cuboidal box = 2[lh + bh]
= [2(12.5
 8 + 10
8 + 10  8)]
8)] 
= 360

The lateral surface area of cubical box is greater than lateral surface area of cuboidal box.
Lateral surface area of cubical box - lateral surface area of cuboidal box = 400
 - 360
- 360  = 40
= 40 
Thus, the lateral surface area of cubical box is greater than that of cuboidal box by 40 cm2.
(ii) Total surface area of cubical box =
 =
=  = 600 cm2
= 600 cm2Total surface area of cuboidal box = 2[lh + bh + lb]
= [2(12.5
 8 + 10
8 + 10  8 + 12.5
8 + 12.5  10]
10]  =
= 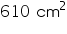
The total surface area of cubical box is smaller than that of cuboidal box
Total surface area of cuboidal box - total surface area of cubical box =
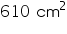 -
- 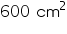 =
=
Thus, the total surface area of cubical box is smaller than that of cuboidal box by

Question 6
A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high.
(i) What is the area of the glass?
(ii) How much of tape is needed for all the 12 edges?
(i) What is the area of the glass?
(ii) How much of tape is needed for all the 12 edges?
Solution 6
(i) Length of green house = 30 cm
Breadth of green house = 25 cm
Height of green house = 25 cm
Total surface area of green house = 2[lb + lh + bh]
= [2(30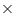 25 + 30
25 + 30  25 + 25
25 + 25  25)]
25)] 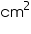
= [2(750 + 750 + 625)]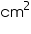
= (2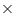 2125)
2125) 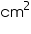
= 4250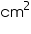
Thus, the area of the glass is 4250 .
.
(ii) Total length of tape = 4(l + b + h)
= [4(30 + 25 + 25)] cm
= 320 cm
Therefore, 320 cm tape is needed for all the 12 edges.
Breadth of green house = 25 cm
Height of green house = 25 cm
Total surface area of green house = 2[lb + lh + bh]
= [2(30
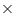 25 + 30
25 + 30 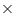 25 + 25
25 + 25 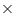 25)]
25)] 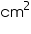
= [2(750 + 750 + 625)]
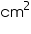
= (2
 2125)
2125) 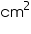
= 4250
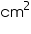
Thus, the area of the glass is 4250
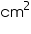 .
.(ii) Total length of tape = 4(l + b + h)
= [4(30 + 25 + 25)] cm
= 320 cm
Therefore, 320 cm tape is needed for all the 12 edges.
Question 7
Shanti Sweets Stall was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 25 cm  20 cm
20 cm  5 cm and the smaller of dimensions 15 cm
5 cm and the smaller of dimensions 15 cm  12 cm
12 cm  5 cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the cardboard is Rs 4 for 1000
5 cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the cardboard is Rs 4 for 1000  , find the cost of cardboard required for supplying 250 boxes of each kind.
, find the cost of cardboard required for supplying 250 boxes of each kind.
 20 cm
20 cm  5 cm and the smaller of dimensions 15 cm
5 cm and the smaller of dimensions 15 cm  12 cm
12 cm  5 cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the cardboard is Rs 4 for 1000
5 cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the cardboard is Rs 4 for 1000  , find the cost of cardboard required for supplying 250 boxes of each kind.
, find the cost of cardboard required for supplying 250 boxes of each kind.
Solution 7
Length of bigger box = 25 cm
Breadth of bigger box = 20 cm
Height of bigger box = 5 cm
Total surface area of bigger box = 2(lb + lh + bh)
= [2(25 20 + 25
20 + 25  5 + 20
5 + 20  5)]
5)] 
= [2(500 + 125 + 100)] cm2 = 1450
Extra area required for overlapping =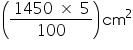 = 72.5
= 72.5 
Considering all overlaps, total surface area of 1 bigger box
= (1450 + 72.5) =1522.5
=1522.5 
Area of cardboard sheet required for 250 such bigger box
= (1522.5 250)
250)  = 380625
= 380625 
Total surface area of smaller box = [2(15 12 + 15
12 + 15  5 + 12
5 + 12  5]
5]  = [2(180 + 75 + 60)]
= [2(180 + 75 + 60)]  = (2
= (2  315)
315)  = 630
= 630 
Extra area required for overlapping =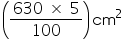 = 31.5
= 31.5 
Considering all overlaps, total surface area of 1 smaller box
= (630 + 31.5) = 661.5
= 661.5 
Area of cardboard sheet required for 250 smaller box
= (250 661.5)
661.5)  = 165375
= 165375 
Total cardboard sheet required = (380625 + 165375) = 546000
= 546000 
Cost of 1000 cardboard sheet = Rs 4
cardboard sheet = Rs 4
Cost of 546000 cardboard sheet = Rs
cardboard sheet = Rs 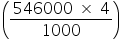 = Rs 2184
= Rs 2184
So, cost of cardboard sheet required for 250 boxes of each kind will be Rs 2184.
Breadth of bigger box = 20 cm
Height of bigger box = 5 cm
Total surface area of bigger box = 2(lb + lh + bh)
= [2(25
 20 + 25
20 + 25  5 + 20
5 + 20  5)]
5)] 
= [2(500 + 125 + 100)] cm2 = 1450

Extra area required for overlapping =
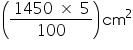 = 72.5
= 72.5 
Considering all overlaps, total surface area of 1 bigger box
= (1450 + 72.5)
 =1522.5
=1522.5 
Area of cardboard sheet required for 250 such bigger box
= (1522.5
 250)
250)  = 380625
= 380625 
Total surface area of smaller box = [2(15
 12 + 15
12 + 15  5 + 12
5 + 12  5]
5]  = [2(180 + 75 + 60)]
= [2(180 + 75 + 60)]  = (2
= (2  315)
315)  = 630
= 630 
Extra area required for overlapping =
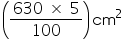 = 31.5
= 31.5 
Considering all overlaps, total surface area of 1 smaller box
= (630 + 31.5)
 = 661.5
= 661.5 
Area of cardboard sheet required for 250 smaller box
= (250
 661.5)
661.5)  = 165375
= 165375 
Total cardboard sheet required = (380625 + 165375)
 = 546000
= 546000 
Cost of 1000
 cardboard sheet = Rs 4
cardboard sheet = Rs 4Cost of 546000
 cardboard sheet = Rs
cardboard sheet = Rs 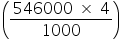 = Rs 2184
= Rs 2184 So, cost of cardboard sheet required for 250 boxes of each kind will be Rs 2184.
Question 8
Parveen wanted to make a temporary shelter for her car, by making a box-like structure with tarpaulin that covers all the four sides and the top of the car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make the shelter of height 2.5 m, with base dimensions 4 m  3 m?
3 m?
 3 m?
3 m?
Solution 8
Length of shelter = 4 m
Breadth of shelter = 3 m
Height of shelter = 2.5 m
The tarpaulin will be required for top and four sides of the shelter.
Area of Tarpaulin required = 2(lh + bh) + lb
= [2(4 2.5 + 3
2.5 + 3  2.5) + 4
2.5) + 4  3]
3] 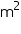
= [2(10 + 7.5) + 12]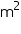
= 47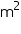
Breadth of shelter = 3 m
Height of shelter = 2.5 m
The tarpaulin will be required for top and four sides of the shelter.
Area of Tarpaulin required = 2(lh + bh) + lb
= [2(4
 2.5 + 3
2.5 + 3  2.5) + 4
2.5) + 4  3]
3] 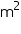
= [2(10 + 7.5) + 12]
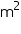
= 47
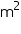
NCERT Solution for Class 9 Mathematics Chapter 13 - Surface Areas and Volumes Page/Excercise 13.2
Question 1
Assume 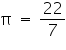 , unless stated otherwise The curved surface area of a right circular cylinder of height 14 cm is 88
, unless stated otherwise The curved surface area of a right circular cylinder of height 14 cm is 88 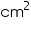 . Find the diameter of the base of the cylinder.
. Find the diameter of the base of the cylinder.
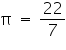 , unless stated otherwise The curved surface area of a right circular cylinder of height 14 cm is 88
, unless stated otherwise The curved surface area of a right circular cylinder of height 14 cm is 88 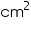 . Find the diameter of the base of the cylinder.
. Find the diameter of the base of the cylinder.
Solution 1
Height of the cylinder = 14 cm
Let diameter of cylinder be d and the radius of its base be r.
Curved surface area of cylinder = 88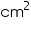
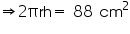
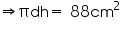
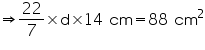
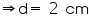
Thus, the diameter of the base of the cylinder is 2 cm.
Let diameter of cylinder be d and the radius of its base be r.
Curved surface area of cylinder = 88
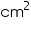
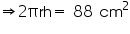
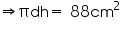
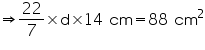
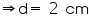
Thus, the diameter of the base of the cylinder is 2 cm.
Question 2
Assume 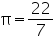 , unless started otherwise. It is required to make a closed cylindrical tank of height 1 m and base diameter 140 cm from a metal sheet. How many square meters of the sheet are required for the same?
, unless started otherwise. It is required to make a closed cylindrical tank of height 1 m and base diameter 140 cm from a metal sheet. How many square meters of the sheet are required for the same?
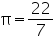 , unless started otherwise. It is required to make a closed cylindrical tank of height 1 m and base diameter 140 cm from a metal sheet. How many square meters of the sheet are required for the same?
, unless started otherwise. It is required to make a closed cylindrical tank of height 1 m and base diameter 140 cm from a metal sheet. How many square meters of the sheet are required for the same?
Solution 2
Height (h) of cylindrical tank = 1 m.
Base radius (r) of cylindrical tank =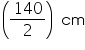 = 70 cm = 0.7 m
= 70 cm = 0.7 m
Area of sheet required = total surface area of tank =
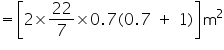
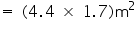

So, it will require 7.48 area of sheet.
area of sheet.
Base radius (r) of cylindrical tank =
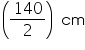 = 70 cm = 0.7 m
= 70 cm = 0.7 m Area of sheet required = total surface area of tank =

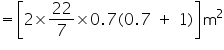
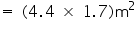

So, it will require 7.48
 area of sheet.
area of sheet.
Question 3
A metal pipe is 77 cm long. The inner diameter of a cross section is 4 cm, the outer diameter being 4.4 cm. Find its
(i) Inner curved surface area, (ii) Outer curved surface area,
(iii) Total surface area. 
(i) Inner curved surface area, (ii) Outer curved surface area,
(iii) Total surface area.
Solution 3
Inner radius  of cylindrical pipe = 2 cm
of cylindrical pipe = 2 cm
Outer radius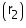 of cylindrical pipe = 2.2 cm
of cylindrical pipe = 2.2 cm
Height (h) of cylindrical pipe = length of cylindrical pipe = 77 cm
(i) CSA of inner surface of pipe =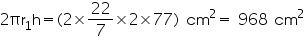
(ii) CSA of outer surface of pipe =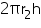
=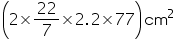 =
= 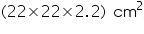 = 1064.8
= 1064.8  (iii) Total surface area of pipe = CSA of inner surface + CSA of outer surface+ area of both circular ends of pipe
(iii) Total surface area of pipe = CSA of inner surface + CSA of outer surface+ area of both circular ends of pipe 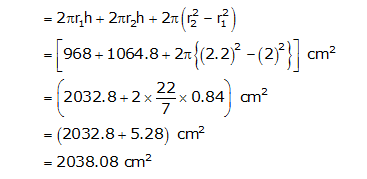
Thus, the total surface area of cylindrical pipe is 2038.08 .
.
 of cylindrical pipe = 2 cm
of cylindrical pipe = 2 cmOuter radius
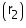 of cylindrical pipe = 2.2 cm
of cylindrical pipe = 2.2 cmHeight (h) of cylindrical pipe = length of cylindrical pipe = 77 cm
(i) CSA of inner surface of pipe =
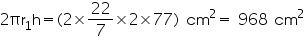
(ii) CSA of outer surface of pipe =
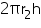
=
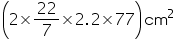 =
= 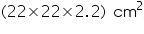 = 1064.8
= 1064.8  (iii) Total surface area of pipe = CSA of inner surface + CSA of outer surface+ area of both circular ends of pipe
(iii) Total surface area of pipe = CSA of inner surface + CSA of outer surface+ area of both circular ends of pipe 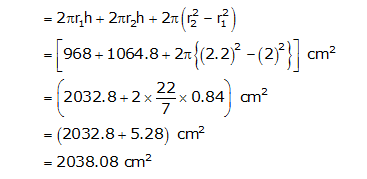
Thus, the total surface area of cylindrical pipe is 2038.08
 .
.
Question 4
Assume 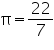 , unless started otherwise The diameter of a roller is 84 cm and its length is 120 cm. It takes 500 complete revolutions to move once over to level a playground. Find the area of the playground in
, unless started otherwise The diameter of a roller is 84 cm and its length is 120 cm. It takes 500 complete revolutions to move once over to level a playground. Find the area of the playground in 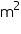 ?
?
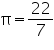 , unless started otherwise The diameter of a roller is 84 cm and its length is 120 cm. It takes 500 complete revolutions to move once over to level a playground. Find the area of the playground in
, unless started otherwise The diameter of a roller is 84 cm and its length is 120 cm. It takes 500 complete revolutions to move once over to level a playground. Find the area of the playground in 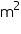 ?
?
Solution 4
The roller is cylindrical.
Height of the roller = length of roller = 120 cm
Radius of the circular end of the roller =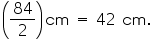
CSA of roller =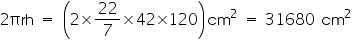
Area of field = 500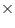 CSA of roller = (500
CSA of roller = (500 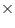 31680)
31680)  = 15840000
= 15840000 
= 1584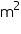
Height of the roller = length of roller = 120 cm
Radius of the circular end of the roller =
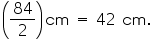
CSA of roller =
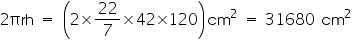
Area of field = 500
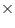 CSA of roller = (500
CSA of roller = (500 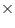 31680)
31680)  = 15840000
= 15840000 
= 1584
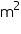
Question 5
Assume 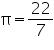 , unless started otherwise A cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the pillar at the rate of Rs.12.50 per
, unless started otherwise A cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the pillar at the rate of Rs.12.50 per  .
.
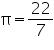 , unless started otherwise A cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the pillar at the rate of Rs.12.50 per
, unless started otherwise A cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the pillar at the rate of Rs.12.50 per  .
.
Solution 5
Height of the pillar = 3.5 m
Radius of the circular end of the pillar =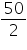 cm = 25 cm = 0.25 m
cm = 25 cm = 0.25 m
CSA of pillar =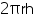 =
= 
Cost of painting 1 area = Rs 12.50
area = Rs 12.50
Cost of painting 5.5 area = Rs (5.5
area = Rs (5.5 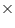 12.50) = Rs 68.75
12.50) = Rs 68.75
Thus, the cost of painting the CSA of pillar is Rs 68.75.
Radius of the circular end of the pillar =
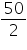 cm = 25 cm = 0.25 m
cm = 25 cm = 0.25 mCSA of pillar =
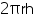 =
= 
Cost of painting 1
 area = Rs 12.50
area = Rs 12.50Cost of painting 5.5
 area = Rs (5.5
area = Rs (5.5 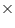 12.50) = Rs 68.75
12.50) = Rs 68.75Thus, the cost of painting the CSA of pillar is Rs 68.75.
Question 6
Assume 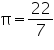 , unless started otherwise Curved surface area of a right circular cylinder is 4.4
, unless started otherwise Curved surface area of a right circular cylinder is 4.4  . If the radius of the base of the cylinder is 0.7 m, find its height.
. If the radius of the base of the cylinder is 0.7 m, find its height.
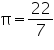 , unless started otherwise Curved surface area of a right circular cylinder is 4.4
, unless started otherwise Curved surface area of a right circular cylinder is 4.4  . If the radius of the base of the cylinder is 0.7 m, find its height.
. If the radius of the base of the cylinder is 0.7 m, find its height.
Solution 6
Let the height of the cylinder be h.
Radius of the base of the cylinder = 0.7 m
CSA of cylinder = 4.4
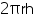 = 4.4
= 4.4 
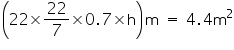
h = 1 m
Thus, the height of the cylinder is 1 m.
Radius of the base of the cylinder = 0.7 m
CSA of cylinder = 4.4

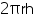 = 4.4
= 4.4 
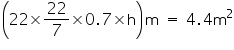
h = 1 m
Thus, the height of the cylinder is 1 m.
Question 7
Assume 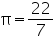 , unless started otherwise The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find
, unless started otherwise The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find
(i) Its inner curved surface area,
(ii) The cost of plastering this curved surface at the rate of Rs 40 per 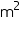
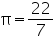 , unless started otherwise The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find
, unless started otherwise The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find(i) Its inner curved surface area,
(ii) The cost of plastering this curved surface at the rate of Rs 40 per
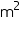
Solution 7
Inner radius (r) of circular well
Depth (h) of circular well = 10 m (i) Inner curved surface area =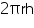
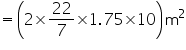
= (44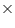 0.25
0.25 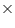 10)
10) 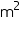
= 110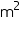
(ii) Cost of plastering 1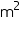 area = Rs 40
area = Rs 40
Cost of plastering 110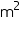 area = Rs (110
area = Rs (110 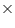 40) = Rs 4400
40) = Rs 4400
Depth (h) of circular well = 10 m (i) Inner curved surface area =
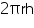
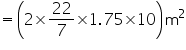
= (44
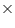 0.25
0.25 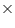 10)
10) 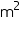
= 110
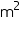
(ii) Cost of plastering 1
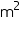 area = Rs 40
area = Rs 40 Cost of plastering 110
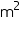 area = Rs (110
area = Rs (110 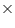 40) = Rs 4400
40) = Rs 4400
Question 8
Assume 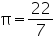 , unless stated otherwise. In a hot water heating system, there is a cylindrical pipe of length 28 m and diameter 5 cm. Find the total radiating surface in the system.
, unless stated otherwise. In a hot water heating system, there is a cylindrical pipe of length 28 m and diameter 5 cm. Find the total radiating surface in the system.
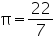 , unless stated otherwise. In a hot water heating system, there is a cylindrical pipe of length 28 m and diameter 5 cm. Find the total radiating surface in the system.
, unless stated otherwise. In a hot water heating system, there is a cylindrical pipe of length 28 m and diameter 5 cm. Find the total radiating surface in the system.
Solution 8
Height (h) of cylindrical pipe = Length of cylindrical pipe = 28 m
Radius (r) of circular end of pipe =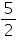 cm = 2.5 cm = 0.025 m
cm = 2.5 cm = 0.025 m
CSA of cylindrical pipe =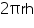
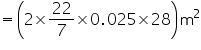 = 4.4
= 4.4 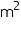
Thus, the area of radiating surface of the system is 4.4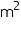 .
.
Radius (r) of circular end of pipe =
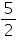 cm = 2.5 cm = 0.025 m
cm = 2.5 cm = 0.025 mCSA of cylindrical pipe =
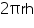
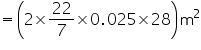 = 4.4
= 4.4 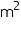
Thus, the area of radiating surface of the system is 4.4
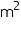 .
.
Question 9
Assume  , unless stated otherwise. Find
, unless stated otherwise. Find
(i) the lateral or curved surface area of a closed cylindrical petrol storage tank that is 4.2 m in diameter and 4.5 m high. (ii) how much steel was actually used, if 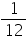 of the steel actually used was wasted in making the tank.
of the steel actually used was wasted in making the tank.
 , unless stated otherwise. Find
, unless stated otherwise. Find(i) the lateral or curved surface area of a closed cylindrical petrol storage tank that is 4.2 m in diameter and 4.5 m high. (ii) how much steel was actually used, if
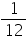 of the steel actually used was wasted in making the tank.
of the steel actually used was wasted in making the tank.
Solution 9
Height (h) cylindrical tank = 4.5 m
Radius (r) of circular end of cylindrical tank = m = 2.1m
m = 2.1m
(i) Lateral or curved surface area of tank =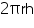
=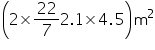
= 59.4 m2
(ii) Total surface area of tank = 2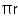 (r + h)
(r + h)
=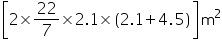
= 87.12 m2
Let A m2 steel sheet be actually used in making the tank.
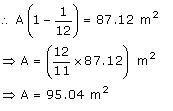
Thus, 95.04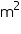 steel was used in actual while making the tank.
steel was used in actual while making the tank.
Radius (r) of circular end of cylindrical tank =
 m = 2.1m
m = 2.1m(i) Lateral or curved surface area of tank =
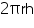
=
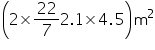
= 59.4 m2
(ii) Total surface area of tank = 2
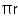 (r + h)
(r + h) =
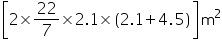
= 87.12 m2
Let A m2 steel sheet be actually used in making the tank.
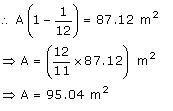
Thus, 95.04
 steel was used in actual while making the tank.
steel was used in actual while making the tank.
Question 10
Assume  , unless started otherwise In the given figure, you see the frame of a lampshade. It is to be covered with a decorative cloth. The frame has a base diameter of 20 cm and height of 30 cm. A margin of 2.5 cm is to be given for folding it over the top and bottom of the frame. Find how much cloth is required for covering the lampshade.
, unless started otherwise In the given figure, you see the frame of a lampshade. It is to be covered with a decorative cloth. The frame has a base diameter of 20 cm and height of 30 cm. A margin of 2.5 cm is to be given for folding it over the top and bottom of the frame. Find how much cloth is required for covering the lampshade. 
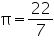 , unless started otherwise In the given figure, you see the frame of a lampshade. It is to be covered with a decorative cloth. The frame has a base diameter of 20 cm and height of 30 cm. A margin of 2.5 cm is to be given for folding it over the top and bottom of the frame. Find how much cloth is required for covering the lampshade.
, unless started otherwise In the given figure, you see the frame of a lampshade. It is to be covered with a decorative cloth. The frame has a base diameter of 20 cm and height of 30 cm. A margin of 2.5 cm is to be given for folding it over the top and bottom of the frame. Find how much cloth is required for covering the lampshade. 
Solution 10
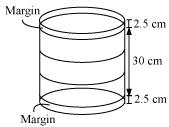 Height of frame of lampshade = (2.5 + 30 + 2.5) cm = 35 cm
Height of frame of lampshade = (2.5 + 30 + 2.5) cm = 35 cmRadius of the circular end of frame of lampshade =
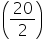 cm = 10cm
cm = 10cmCloth required for covering the lampshade =


= 2200
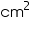
Thus, for covering the lampshade 2200
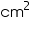 cloth will be required.
cloth will be required.
Question 11
Assume 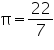 , unless started otherwise The students of a Vidyalaya were asked to participate in a competition for making and decorating penholders in the shape of a cylinder with a base, using cardboard. Each penholder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition?
, unless started otherwise The students of a Vidyalaya were asked to participate in a competition for making and decorating penholders in the shape of a cylinder with a base, using cardboard. Each penholder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition?
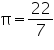 , unless started otherwise The students of a Vidyalaya were asked to participate in a competition for making and decorating penholders in the shape of a cylinder with a base, using cardboard. Each penholder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition?
, unless started otherwise The students of a Vidyalaya were asked to participate in a competition for making and decorating penholders in the shape of a cylinder with a base, using cardboard. Each penholder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition?
Solution 11
Radius of circular end of cylindrical penholder = 3 cm
Height of penholder = 10.5 cm
Surface area of 1 penholder = CSA of penholder + Area of base of penholder =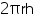 +
+ 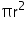
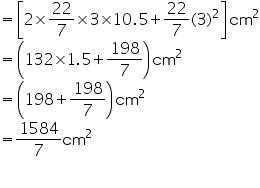
Area of cardboard sheet used by 1 competitor =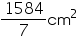
Area of cardboard sheet used by 35 competitors
 = 7920 cm2
= 7920 cm2
Thus, 7920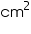 cardboard sheet will be bought for the competition.
cardboard sheet will be bought for the competition.
Height of penholder = 10.5 cm
Surface area of 1 penholder = CSA of penholder + Area of base of penholder =
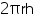 +
+ 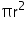
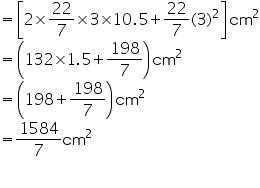
Area of cardboard sheet used by 1 competitor =
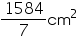
Area of cardboard sheet used by 35 competitors
 = 7920 cm2
= 7920 cm2Thus, 7920
 cardboard sheet will be bought for the competition.
cardboard sheet will be bought for the competition.NCERT Solution for Class 9 Mathematics Chapter 13 - Surface Areas and Volumes Page/Excercise 13.3
Question 1
Assume 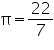 , unless started otherwise Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
, unless started otherwise Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
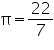 , unless started otherwise Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
, unless started otherwise Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
Solution 1
Radius of base of cone = 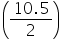 cm = 5.25 cm
cm = 5.25 cm
Slant height of cone = 10 cm
CSA of cone =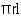 =
= 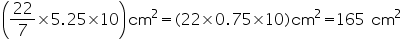
Thus, the curved surface area of cone is 165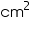 .
.
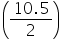 cm = 5.25 cm
cm = 5.25 cmSlant height of cone = 10 cm
CSA of cone =
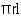 =
= 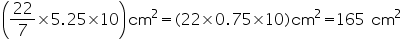
Thus, the curved surface area of cone is 165
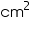 .
.
Question 2
Assume 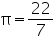 , unless stated otherwise. Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
, unless stated otherwise. Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
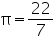 , unless stated otherwise. Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
, unless stated otherwise. Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
Solution 2
Radius of base of cone = 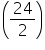 m = 12 cm
m = 12 cm
Slant height of cone = 21 m
Total surface area of cone =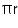 (r + l)
(r + l)
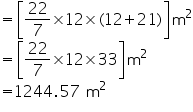
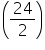 m = 12 cm
m = 12 cmSlant height of cone = 21 m
Total surface area of cone =
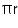 (r + l)
(r + l) 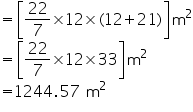
Question 3
Assume 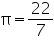 , unless stated otherwise. Curved surface area of a cone is 308
, unless stated otherwise. Curved surface area of a cone is 308 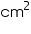 and its slant height is 14 cm. Find
and its slant height is 14 cm. Find
(i) radius of the base and (ii) total surface area of the cone.
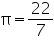 , unless stated otherwise. Curved surface area of a cone is 308
, unless stated otherwise. Curved surface area of a cone is 308 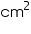 and its slant height is 14 cm. Find
and its slant height is 14 cm. Find(i) radius of the base and (ii) total surface area of the cone.
Solution 3
(i) Slant height of cone = 14 cm
Let radius of circular end of cone be r.
CSA of cone =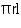
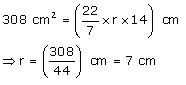
Thus, the radius of circular end of the cone is 7 cm.
(ii) Total surface area of cone = CSA of cone + Area of base
=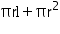
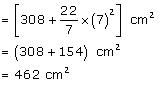 Thus, the total surface area of the cone is 462
Thus, the total surface area of the cone is 462 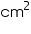 .
.
Let radius of circular end of cone be r.
CSA of cone =
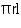
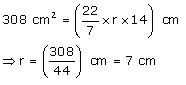
Thus, the radius of circular end of the cone is 7 cm.
(ii) Total surface area of cone = CSA of cone + Area of base
=
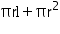
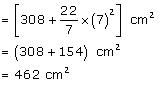 Thus, the total surface area of the cone is 462
Thus, the total surface area of the cone is 462 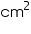 .
.
Question 4
Assume 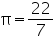 , unless stated otherwise. A conical tent is 10 m high and the radius of its base is 24 m. Find
, unless stated otherwise. A conical tent is 10 m high and the radius of its base is 24 m. Find
(i) Slant height of the tent (ii) Cost of the canvas required to make the tent, if the cost of 1 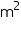 canvas is Rs 70.
canvas is Rs 70.
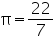 , unless stated otherwise. A conical tent is 10 m high and the radius of its base is 24 m. Find
, unless stated otherwise. A conical tent is 10 m high and the radius of its base is 24 m. Find(i) Slant height of the tent (ii) Cost of the canvas required to make the tent, if the cost of 1
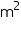 canvas is Rs 70.
canvas is Rs 70.
Solution 4
(i) Height (h) of conical tent = 10 m
Radius (r) of conical tent = 24 m
Let slant height of conical tent be l.
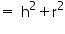
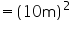

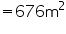
 l = 26 m . Thus, the slant height of the conical tent is 26 m.
l = 26 m . Thus, the slant height of the conical tent is 26 m.
(ii) CSA of tent =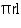 =
= 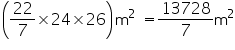
Cost of 1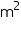 canvas = Rs 70
canvas = Rs 70
Cost of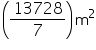 canvas =
canvas = 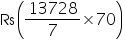 = Rs 137280
= Rs 137280
Thus, the cost of canvas required to make the tent is Rs 137280.
Radius (r) of conical tent = 24 m
Let slant height of conical tent be l.
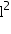
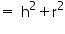
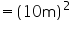

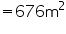
(ii) CSA of tent =
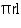 =
= 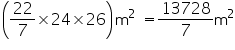
Cost of 1
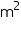 canvas = Rs 70
canvas = Rs 70Cost of
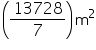 canvas =
canvas = 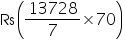 = Rs 137280
= Rs 137280Thus, the cost of canvas required to make the tent is Rs 137280.
Question 5
Assume 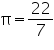 , unless stated otherwise. What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. (Use
, unless stated otherwise. What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. (Use 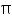 = 3.14).
= 3.14).
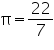 , unless stated otherwise. What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. (Use
, unless stated otherwise. What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. (Use 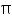 = 3.14).
= 3.14).
Solution 5
Height (h) of conical tent = 8 m
Radius (r) of base of tent = 6 m
Slant height (l) of tent =
CSA of conical tent =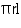 = (3.14
= (3.14  6
6  10)
10) 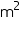 = 188.4
= 188.4 
Let length of tarpaulin sheet required be L.
As 20 cm will be wasted so, effective length will be (L - 0.2 m)
Breadth of tarpaulin = 3 m
Area of sheet = CSA of tent
[(L - 0.2 m)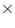 3] m = 188.4
3] m = 188.4 
L - 0.2 m = 62.8 m
L = 63 m
Thus, the length of the tarpaulin sheet will be 63 m.
Radius (r) of base of tent = 6 m
Slant height (l) of tent =

CSA of conical tent =
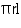 = (3.14
= (3.14  6
6  10)
10) 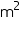 = 188.4
= 188.4 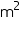
Let length of tarpaulin sheet required be L.
As 20 cm will be wasted so, effective length will be (L - 0.2 m)
Breadth of tarpaulin = 3 m
Area of sheet = CSA of tent
[(L - 0.2 m)
 3] m = 188.4
3] m = 188.4 
L - 0.2 m = 62.8 m
L = 63 m
Thus, the length of the tarpaulin sheet will be 63 m.
Question 6
Assume 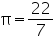 , unless stated otherwise. The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs 210 per 100
, unless stated otherwise. The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs 210 per 100 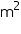 .
.
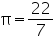 , unless stated otherwise. The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs 210 per 100
, unless stated otherwise. The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs 210 per 100 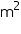 .
.
Solution 6
Slant height (l) of conical tomb = 25 m
Base radius (r) of tomb = = 7 m
= 7 m
CSA of conical tomb =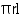 =
=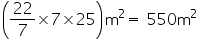
Cost of white-washing 100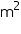 area = Rs 210
area = Rs 210
Cost of white-washing 550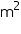 area =Rs
area =Rs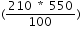 = Rs 1155
= Rs 1155
Thus, the cost of white washing the conical tomb is Rs 1155.
Base radius (r) of tomb =
 = 7 m
= 7 mCSA of conical tomb =
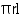 =
=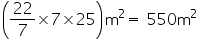
Cost of white-washing 100
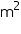 area = Rs 210
area = Rs 210Cost of white-washing 550
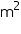 area =Rs
area =Rs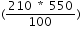 = Rs 1155
= Rs 1155Thus, the cost of white washing the conical tomb is Rs 1155.
Question 7
Assume  , unless stated otherwise. A joker's cap is in the form of right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
, unless stated otherwise. A joker's cap is in the form of right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
 , unless stated otherwise. A joker's cap is in the form of right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
, unless stated otherwise. A joker's cap is in the form of right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
Solution 7
Radius (r) of conical cap = 7 cm
Height (h) of conical cap = 24 cm
Slant height (l) of conical cap =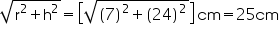
CSA of 1 conical cap =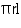 =
= 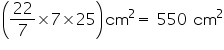
CSA of 10 such conical caps = (10 550)
550)  = 5500
= 5500 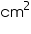
Thus, 5500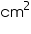 sheet will be required to make the 10 caps.
sheet will be required to make the 10 caps.
Height (h) of conical cap = 24 cm
Slant height (l) of conical cap =
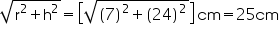
CSA of 1 conical cap =
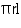 =
= 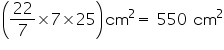
CSA of 10 such conical caps = (10
 550)
550)  = 5500
= 5500 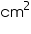
Thus, 5500
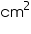 sheet will be required to make the 10 caps.
sheet will be required to make the 10 caps.
Question 8
Assume 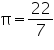 , unless stated otherwise. A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. if the outer side of each of the cones is to be painted and the cost of painting is Rs 12 per
, unless stated otherwise. A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. if the outer side of each of the cones is to be painted and the cost of painting is Rs 12 per 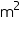 , what will be the cost of painting all these cones? (Use
, what will be the cost of painting all these cones? (Use 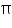 = 3.14 and take
= 3.14 and take 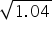 = 1.02).
= 1.02).
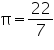 , unless stated otherwise. A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. if the outer side of each of the cones is to be painted and the cost of painting is Rs 12 per
, unless stated otherwise. A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. if the outer side of each of the cones is to be painted and the cost of painting is Rs 12 per 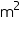 , what will be the cost of painting all these cones? (Use
, what will be the cost of painting all these cones? (Use 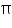 = 3.14 and take
= 3.14 and take 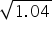 = 1.02).
= 1.02).
Solution 8
Radius (r) of cone =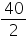 = 0.2 m
= 0.2 m
Height (h) of cone = 1 m
Slant height (l) of cone =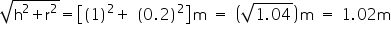
CSA of each cone = = (3.14
= (3.14 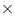 0.2
0.2  1.02)
1.02)  = 0.64056
= 0.64056 
CSA of 50 such cones = (50 0.64056)
0.64056) 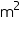 = 32.028
= 32.028 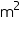
Cost of painting 1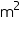 area = Rs 12
area = Rs 12
Cost of painting 32.028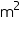 area = Rs (32.028
area = Rs (32.028 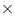 12) = Rs 384.336
12) = Rs 384.336
Thus, it will cost Rs 384.34 (approximately) in painting the 50 hollow cones.
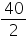 = 0.2 m
= 0.2 mHeight (h) of cone = 1 m
Slant height (l) of cone =
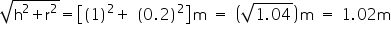
CSA of each cone =
 = (3.14
= (3.14 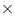 0.2
0.2  1.02)
1.02) 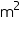 = 0.64056
= 0.64056 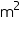
CSA of 50 such cones = (50
 0.64056)
0.64056) 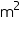 = 32.028
= 32.028 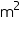
Cost of painting 1
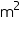 area = Rs 12
area = Rs 12Cost of painting 32.028
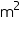 area = Rs (32.028
area = Rs (32.028 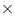 12) = Rs 384.336
12) = Rs 384.336Thus, it will cost Rs 384.34 (approximately) in painting the 50 hollow cones.
NCERT Solution for Class 9 Mathematics Chapter 13 - Surface Areas and Volumes Page/Excercise 13.4
Question 1
Assume 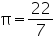 , unless stated otherwise.
, unless stated otherwise.
Find the surface area of a sphere of radius:
(i) 10.5 cm (ii) 5.6 cm (iii) 14 cm
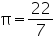 , unless stated otherwise.
, unless stated otherwise.Find the surface area of a sphere of radius:
(i) 10.5 cm (ii) 5.6 cm (iii) 14 cm
Solution 1
(i) Radius of sphere = 10.5 cm
Surface area of sphere =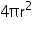

Surface area of sphere =
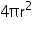

(ii) Radius of sphere = 5.6 cm
Surface area of sphere =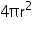 =
= 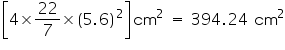
Surface area of sphere =
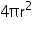 =
= 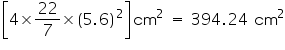
(iii) Radius of sphere = 14 cm
Surface area of sphere = =
= 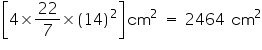
Surface area of sphere =
 =
= 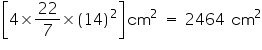
Question 2
Assume 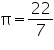 , unless stated otherwise.
, unless stated otherwise.
Find the surface area of a sphere of diameter:
(i) 14 cm (ii) 21 cm (iii) 3.5 m
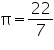 , unless stated otherwise.
, unless stated otherwise.Find the surface area of a sphere of diameter:
(i) 14 cm (ii) 21 cm (iii) 3.5 m
Solution 2
(i) Radius of sphere 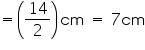
Surface area of sphere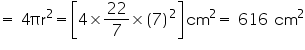
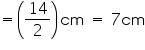
Surface area of sphere
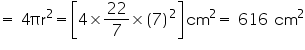
(ii) Radius of sphere 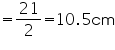
Surface area of sphere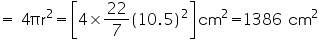
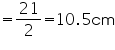
Surface area of sphere
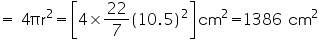
(iii) Radius of sphere 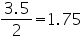
Surface area of sphere =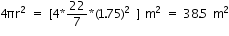
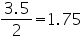
Surface area of sphere =
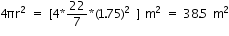
Question 3
Assume  , unless stated otherwise. Find the total surface area of a hemisphere of radius 10 cm. (Use
, unless stated otherwise. Find the total surface area of a hemisphere of radius 10 cm. (Use 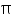 = 3.14)
= 3.14)
 , unless stated otherwise. Find the total surface area of a hemisphere of radius 10 cm. (Use
, unless stated otherwise. Find the total surface area of a hemisphere of radius 10 cm. (Use 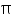 = 3.14)
= 3.14)
Solution 3
Radius of hemisphere = 10 cm
Total surface area of hemisphere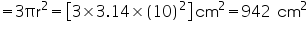
Total surface area of hemisphere
Question 4
Assume 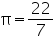 , unless stated otherwise. The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
, unless stated otherwise. The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
 , unless stated otherwise. The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
, unless stated otherwise. The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Solution 4
Radius  of spherical balloon = 7 cm
of spherical balloon = 7 cm
Radius of spherical balloon, when air is pumped into it = 14 cm
of spherical balloon, when air is pumped into it = 14 cm
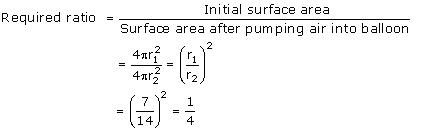
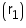 of spherical balloon = 7 cm
of spherical balloon = 7 cmRadius
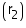 of spherical balloon, when air is pumped into it = 14 cm
of spherical balloon, when air is pumped into it = 14 cm 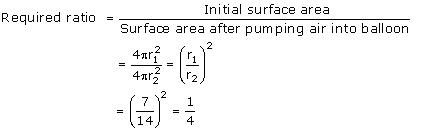
Question 5
Assume 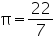 , unless stated otherwise. A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of Rs 16 per 100
, unless stated otherwise. A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of Rs 16 per 100 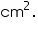
 , unless stated otherwise. A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of Rs 16 per 100
, unless stated otherwise. A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of Rs 16 per 100 
Solution 5
Inner radius (r) of hemispherical bowl = 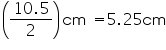
Surface area of hemispherical bowl =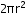
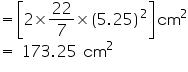
Cost of tin-plating 100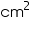 area = Rs 16
area = Rs 16
Cost of tin-plating 173.25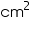 area
area 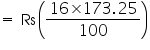 = Rs 27.72 Thus, the cost of tin-plating the inner side of hemispherical bowl is Rs 27.72
= Rs 27.72 Thus, the cost of tin-plating the inner side of hemispherical bowl is Rs 27.72
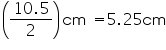
Surface area of hemispherical bowl =
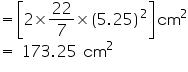
Cost of tin-plating 100
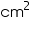 area = Rs 16
area = Rs 16Cost of tin-plating 173.25
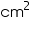 area
area 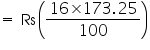 = Rs 27.72 Thus, the cost of tin-plating the inner side of hemispherical bowl is Rs 27.72
= Rs 27.72 Thus, the cost of tin-plating the inner side of hemispherical bowl is Rs 27.72
Question 6
Assume 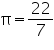 , unless stated otherwise. Find the radius of a sphere whose surface area is 154
, unless stated otherwise. Find the radius of a sphere whose surface area is 154 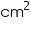 .
.
 , unless stated otherwise. Find the radius of a sphere whose surface area is 154
, unless stated otherwise. Find the radius of a sphere whose surface area is 154 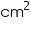 .
.
Solution 6
Let radius of the sphere be r.
Surface area of the sphere = 154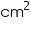
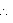
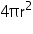 = 154 cm2
= 154 cm2
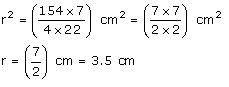
Thus, the radius of the sphere is 3.5 cm.
Surface area of the sphere = 154
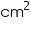
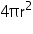 = 154 cm2
= 154 cm2 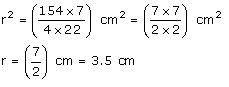
Thus, the radius of the sphere is 3.5 cm.
Question 7
Assume 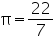 , unless stated otherwise. The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface area.
, unless stated otherwise. The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface area.
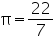 , unless stated otherwise. The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface area.
, unless stated otherwise. The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface area.
Solution 7
Let diameter of earth be d. Then, diameter of moon will be 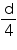 .
.
Radius of earth =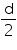
Radius of moon =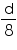
Surface area of moon =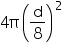
Surface area of earth =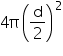
Required ratio =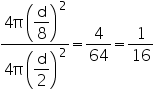
Thus, the required ratio of the surface areas is 1:16.
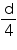 .
.Radius of earth =
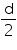
Radius of moon =
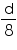
Surface area of moon =
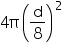
Surface area of earth =
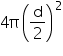
Required ratio =
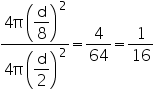
Thus, the required ratio of the surface areas is 1:16.
Question 8
Assume 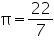 , unless stated otherwise. A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
, unless stated otherwise. A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
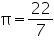 , unless stated otherwise. A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
, unless stated otherwise. A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
Solution 8
Inner radius of hemispherical bowl = 5 cm
Thickness of the bowl = 0.25 cm
 Outer radius (r) of hemispherical bowl = (5 + 0.25) cm = 5.25 cm
Outer radius (r) of hemispherical bowl = (5 + 0.25) cm = 5.25 cm
Outer CSA of hemispherical bowl =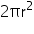
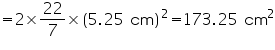
Thus, the outer curved surface area of the bowl is 173.25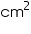 .
.
Thickness of the bowl = 0.25 cm
Outer CSA of hemispherical bowl =
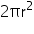
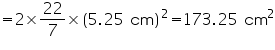
Thus, the outer curved surface area of the bowl is 173.25
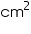 .
.
Question 9
Assume 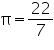 , unless stated otherwise. A right circular cylinder just encloses a sphere of radius r. Find
, unless stated otherwise. A right circular cylinder just encloses a sphere of radius r. Find 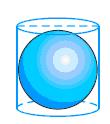 (i) Surface area of the sphere,
(i) Surface area of the sphere,
(ii) Curved surface area of the cylinder,
(iii) Ratio of the areas obtained in (i) and (ii).
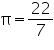 , unless stated otherwise. A right circular cylinder just encloses a sphere of radius r. Find
, unless stated otherwise. A right circular cylinder just encloses a sphere of radius r. Find  (i) Surface area of the sphere,
(i) Surface area of the sphere, (ii) Curved surface area of the cylinder,
(iii) Ratio of the areas obtained in (i) and (ii).
Solution 9
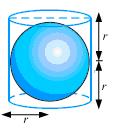 (i) Surface area of sphere =
(i) Surface area of sphere = 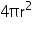
(ii) Height of cylinder = r + r = 2r
Radius of cylinder = r
CSA of cylinder =
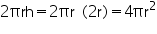
(iii) Required ratio =

NCERT Solution for Class 9 Mathematics Chapter 13 - Surface Areas and Volumes Page/Excercise 13.5
Question 1
A matchbox measures 4 cm 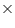 2.5 cm
2.5 cm 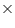 1.5 cm. What will be the volume of a packet containing 12 such boxes?
1.5 cm. What will be the volume of a packet containing 12 such boxes?
 2.5 cm
2.5 cm  1.5 cm. What will be the volume of a packet containing 12 such boxes?
1.5 cm. What will be the volume of a packet containing 12 such boxes?
Solution 1
A matchbox is cuboidal in shape.
Volume of 1 match box = l b
b  h = (4
h = (4  2.5
2.5  1.5)
1.5)  = 15
= 15 
Volume of the packet containing 12 such matchboxes = 12 15
15  =180
=180 
Volume of 1 match box = l
 b
b  h = (4
h = (4  2.5
2.5  1.5)
1.5)  = 15
= 15 
Volume of the packet containing 12 such matchboxes = 12
 15
15  =180
=180 
Question 2
A cuboidal water tank is 6 m long, 5 m wide and 4.5 m deep. How, many litres of water can it holds? (1 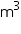 = 1000l)
= 1000l)
 = 1000l)
= 1000l)
Solution 2
Volume of tank = l  b
b  h = (6
h = (6  5
5  4.5)
4.5) 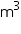 = 135
= 135 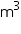 It is given that:
It is given that:
1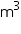 = 1000 litres
= 1000 litres
Thus, the tank can hold 135000 litres of water.
 b
b  h = (6
h = (6  5
5  4.5)
4.5) 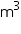 = 135
= 135 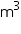 It is given that:
It is given that:1
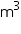 = 1000 litres
= 1000 litresThus, the tank can hold 135000 litres of water.
Question 3
A cuboidal vessel is 10 m long and 8 m wide. How high must it be made to hold 380 cubic metres of a liquid?
Solution 3
Let height of cuboidal vessel be h.
Length (l) of vessel = 10 m
Width (b) of vessel = 8 m
Volume of vessel = 380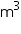
 l
l  b
b  h = 380
h = 380
10 8
8  h = 380
h = 380
h = 4.75
Thus, the height of the vessel should be 4.75 m.
Length (l) of vessel = 10 m
Width (b) of vessel = 8 m
Volume of vessel = 380
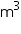
 b
b  h = 380
h = 380 10
 8
8  h = 380
h = 380 h = 4.75
Thus, the height of the vessel should be 4.75 m.
Question 4
Find the cost of digging a cuboidal pit 8 m long, 6 m broad and 3 m deep at the rate of Rs 30 per  .
.
 .
.
Solution 4
Length (l) of the cuboidal pit = 8 m
Width (b) of the cuboidal pit = 6 m
Depth (h) of the cuboidal pit = 3 m
Volume of the cuboidal pit = l b
b  h = (8
h = (8  6
6  3)
3)  = 144
= 144 
Cost of digging 1 = Rs 30
= Rs 30
Cost of digging 144 = Rs (144
= Rs (144  30) = Rs 4320
30) = Rs 4320
Width (b) of the cuboidal pit = 6 m
Depth (h) of the cuboidal pit = 3 m
Volume of the cuboidal pit = l
 b
b  h = (8
h = (8  6
6  3)
3)  = 144
= 144 
Cost of digging 1
 = Rs 30
= Rs 30Cost of digging 144
 = Rs (144
= Rs (144  30) = Rs 4320
30) = Rs 4320
Question 5
The capacity of a cuboidal tank is 50000 litres of water. Find the breadth of the tank, if its length and depth are respectively 2.5 m and 10 m.
Solution 5
Let the breadth of the tank be 'b' m.
Length (l) of the tank = 2.5 m
Depth (h) of the tank = 10 m Volume of tank = l b
b  h = (2.5
h = (2.5  b
b 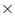 10)
10)  = 25b
= 25b 
Capacity of tank = 25b = 25000 b litres
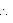 25000 b = 50000 (Given)
25000 b = 50000 (Given)  Thus, the breadth of the tank is 2 m.
Thus, the breadth of the tank is 2 m.
Length (l) of the tank = 2.5 m
Depth (h) of the tank = 10 m Volume of tank = l
 b
b  h = (2.5
h = (2.5  b
b 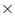 10)
10) 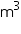 = 25b
= 25b 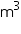
Capacity of tank = 25b = 25000 b litres
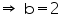 Thus, the breadth of the tank is 2 m.
Thus, the breadth of the tank is 2 m.
Question 6
A village, having a population of 4000, requires 150 litres of water per head per day. It has a tank measuring 20 m  15 m
15 m  6 m. For how many days will the water of this tank last?
6 m. For how many days will the water of this tank last?
 15 m
15 m  6 m. For how many days will the water of this tank last?
6 m. For how many days will the water of this tank last?
Solution 6
Length (l) of the cuboidal tank = 20 m
Breadth (b) of the cuboidal tank = 15 m
Height (h) of the cuboidal tank = 6 m
Capacity of tank = l b
b h = (20
h = (20  15
15  6)
6)  = 1800
= 1800  = 1800000 litres
= 1800000 litres
Water consumed by people of village in 1 day = 4000 150 litres = 600000 litres
150 litres = 600000 litres
Let water of this tank lasts for n days.
Water consumed by all people of village in n days = capacity of tank
n 600000 = 1800000
600000 = 1800000
n = 3
Thus, the water of tank will last for 3 days.
Breadth (b) of the cuboidal tank = 15 m
Height (h) of the cuboidal tank = 6 m
Capacity of tank = l
 b
b h = (20
h = (20  15
15  6)
6)  = 1800
= 1800  = 1800000 litres
= 1800000 litresWater consumed by people of village in 1 day = 4000
 150 litres = 600000 litres
150 litres = 600000 litresLet water of this tank lasts for n days.
Water consumed by all people of village in n days = capacity of tank
n
 600000 = 1800000
600000 = 1800000n = 3
Thus, the water of tank will last for 3 days.
Question 7
A godown measures 40 m  25 m
25 m  10 m. Find the maximum number of wooden crates each measuring 1.5 m
10 m. Find the maximum number of wooden crates each measuring 1.5 m  1.25 m
1.25 m  0.5 m that can be stored in the godown.
0.5 m that can be stored in the godown.
 25 m
25 m  10 m. Find the maximum number of wooden crates each measuring 1.5 m
10 m. Find the maximum number of wooden crates each measuring 1.5 m  1.25 m
1.25 m  0.5 m that can be stored in the godown.
0.5 m that can be stored in the godown.
Solution 7
Length  of the godown = 40 m
of the godown = 40 m
Breadth of the godown = 25 m
of the godown = 25 m
Height of the godown = 10 m
of the godown = 10 m
Volume of godown = l1 b1
b1 h1 = (40
h1 = (40  25
25  10)
10) 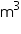 = 10000
= 10000 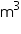
Length of a wooden crate = 1.5 m
of a wooden crate = 1.5 m
Breadth of a wooden crate = 1.25 m
of a wooden crate = 1.25 m
Height of a wooden crate = 0.5 m
of a wooden crate = 0.5 m
Volume of a wooden crate =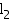

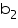

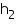 = (1.5
= (1.5  1.25
1.25  0.5) m3 = 0.9375
0.5) m3 = 0.9375 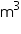
Let n wooden crates be stored in the godown.
Volume of n wooden crates = volume of godown
0.9375 n = 10000
n = 10000
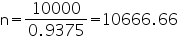
Thus, 10666 number of wooden crates can be stored in godown.
 of the godown = 40 m
of the godown = 40 mBreadth
 of the godown = 25 m
of the godown = 25 mHeight
 of the godown = 10 m
of the godown = 10 mVolume of godown = l1
 b1
b1 h1 = (40
h1 = (40  25
25  10)
10) 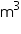 = 10000
= 10000 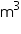
Length
 of a wooden crate = 1.5 m
of a wooden crate = 1.5 mBreadth
 of a wooden crate = 1.25 m
of a wooden crate = 1.25 mHeight
 of a wooden crate = 0.5 m
of a wooden crate = 0.5 mVolume of a wooden crate =
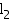

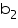

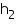 = (1.5
= (1.5  1.25
1.25  0.5) m3 = 0.9375
0.5) m3 = 0.9375 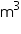
Let n wooden crates be stored in the godown.
Volume of n wooden crates = volume of godown
0.9375
 n = 10000
n = 10000 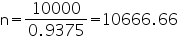
Thus, 10666 number of wooden crates can be stored in godown.
Question 8
A solid cube of side 12 cm is cut into eight cubes of equal volume. What will be the side of the new cube? Also, find the ratio between their surface areas.
Solution 8
Side (a) of the cube = 12 cm
Volume of the cube = a3= (12 cm)3 = 1728
Let the side of each smaller cube be l. Volume of each smaller cube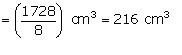

 l = 6 cm
l = 6 cm
Thus, the side of each smaller cube is 6 cm.
Ratio between surface areas of the cubes =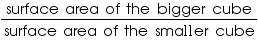
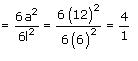
So, the required ratio between surface areas of the cubes is 4 : 1.
Volume of the cube = a3= (12 cm)3 = 1728
Let the side of each smaller cube be l. Volume of each smaller cube
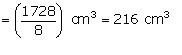

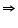 l = 6 cm
l = 6 cmThus, the side of each smaller cube is 6 cm.
Ratio between surface areas of the cubes =
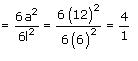
So, the required ratio between surface areas of the cubes is 4 : 1.
Question 9
A river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much water will fall into the sea in a minute?
Solution 9
Rate of water flow = 2 km per hour 
Depth (h) of river = 3 m
Width (b) of river = 40 m
Volume of water flowed in 1 min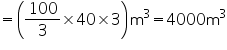
Thus, in 1 minute 4000 water will fall into the sea.
water will fall into the sea.

Depth (h) of river = 3 m
Width (b) of river = 40 m
Volume of water flowed in 1 min
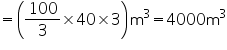
Thus, in 1 minute 4000
 water will fall into the sea.
water will fall into the sea. NCERT Solution for Class 9 Mathematics Chapter 13 - Surface Areas and Volumes Page/Excercise 13.6
Question 1
Assume 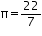 , unless stated otherwise. The circumference of the base of cylindrical vessel is 132 cm and its height is 25 cm. How, many litres of water can it holds? (1000 cm3 = 1l)
, unless stated otherwise. The circumference of the base of cylindrical vessel is 132 cm and its height is 25 cm. How, many litres of water can it holds? (1000 cm3 = 1l)
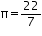 , unless stated otherwise. The circumference of the base of cylindrical vessel is 132 cm and its height is 25 cm. How, many litres of water can it holds? (1000 cm3 = 1l)
, unless stated otherwise. The circumference of the base of cylindrical vessel is 132 cm and its height is 25 cm. How, many litres of water can it holds? (1000 cm3 = 1l)
Solution 1
Let the radius of the cylindrical vessel be r.
Height (h) of the vessel = 25 cm
Circumference of the vessel = 132 cm
2 r = 132 cm
r = 132 cm 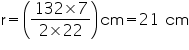 Volume of cylindrical vessel =
Volume of cylindrical vessel =  r2h
r2h 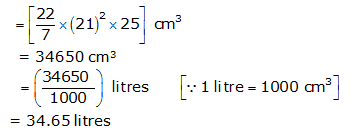 Thus, the vessel can hold 34.65 litres of water.
Thus, the vessel can hold 34.65 litres of water.
Height (h) of the vessel = 25 cm
Circumference of the vessel = 132 cm
2
 r = 132 cm
r = 132 cm 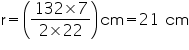 Volume of cylindrical vessel =
Volume of cylindrical vessel =  r2h
r2h 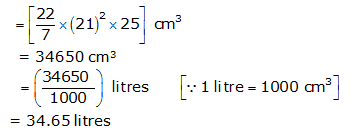 Thus, the vessel can hold 34.65 litres of water.
Thus, the vessel can hold 34.65 litres of water.
Question 2
Assume 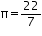 , unless stated otherwise.
, unless stated otherwise.
The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. find the mass of the pipe, if 1 cm3 of wood has a mass of 0.6 g.
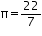 , unless stated otherwise.
, unless stated otherwise.The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. find the mass of the pipe, if 1 cm3 of wood has a mass of 0.6 g.
Solution 2
Inner radius (r1) of cylindrical pipe = 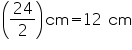 Outer radius (r2) of cylindrical pipe =
Outer radius (r2) of cylindrical pipe = 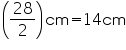 Height (h) of pipe = Length of pipe = 35 cm
Height (h) of pipe = Length of pipe = 35 cm
Volume of pipe = Mass of 1 cm3 wood = 0.6 g
Mass of 1 cm3 wood = 0.6 g
Mass of 5720 cm3 wood = 5720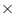 0.6 g = 3432 g = 3.432 kg
0.6 g = 3432 g = 3.432 kg
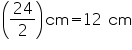 Outer radius (r2) of cylindrical pipe =
Outer radius (r2) of cylindrical pipe = 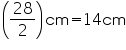 Height (h) of pipe = Length of pipe = 35 cm
Height (h) of pipe = Length of pipe = 35 cmVolume of pipe =
 Mass of 1 cm3 wood = 0.6 g
Mass of 1 cm3 wood = 0.6 gMass of 5720 cm3 wood = 5720
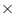 0.6 g = 3432 g = 3.432 kg
0.6 g = 3432 g = 3.432 kg
Question 3
Assume  , unless stated otherwise.
, unless stated otherwise.
A soft drink is available in two packs -
(i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and (ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
 , unless stated otherwise.
, unless stated otherwise.A soft drink is available in two packs -
(i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and (ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
Solution 3
The tin can will be cuboidal in shape. Length (l) of tin can = 5 cm
Breadth (b) of tin can = 4 cm
Height (h) of tin can = 15 cm
Capacity of tin can = l b
b  h = (5
h = (5  4
4  15) cm3 = 300 cm3 Radius (R) of circular end of plastic cylinder =
15) cm3 = 300 cm3 Radius (R) of circular end of plastic cylinder = 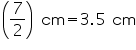 Height (H) of plastic cylinder = 10 cm Capacity of plastic cylinder =
Height (H) of plastic cylinder = 10 cm Capacity of plastic cylinder =  R2H =
R2H = =385 cm3 Thus, the plastic cylinder has greater capacity.
=385 cm3 Thus, the plastic cylinder has greater capacity.
Difference in capacity = (385 - 300) cm3 = 85 cm3
Breadth (b) of tin can = 4 cm
Height (h) of tin can = 15 cm
Capacity of tin can = l
 b
b  h = (5
h = (5  4
4 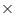 15) cm3 = 300 cm3 Radius (R) of circular end of plastic cylinder =
15) cm3 = 300 cm3 Radius (R) of circular end of plastic cylinder = 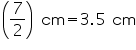 Height (H) of plastic cylinder = 10 cm Capacity of plastic cylinder =
Height (H) of plastic cylinder = 10 cm Capacity of plastic cylinder = 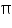 R2H =
R2H = =385 cm3 Thus, the plastic cylinder has greater capacity.
=385 cm3 Thus, the plastic cylinder has greater capacity.Difference in capacity = (385 - 300) cm3 = 85 cm3
Question 4
Assume  , unless stated otherwise.
, unless stated otherwise.
If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, then find
(i) radius of its base (ii) its volume. (Use 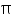 = 3.14)
= 3.14)
 , unless stated otherwise.
, unless stated otherwise.If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, then find
(i) radius of its base (ii) its volume. (Use
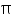 = 3.14)
= 3.14)
Solution 4
(i) Height (h) of cylinder = 5 cm
Let radius of cylinder be r.
CSA of cylinder = 94.2 cm2
2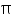 rh = 94.2 cm2
rh = 94.2 cm2
(2 3.14
3.14  r
r  5) cm = 94.2 cm2
5) cm = 94.2 cm2
r = 3 cm (ii) Volume of cylinder =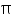 r2h = (3.14
r2h = (3.14  (3)2
(3)2  5) cm3 = 141.3 cm3
5) cm3 = 141.3 cm3
Let radius of cylinder be r.
CSA of cylinder = 94.2 cm2
2
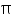 rh = 94.2 cm2
rh = 94.2 cm2(2
 3.14
3.14  r
r  5) cm = 94.2 cm2
5) cm = 94.2 cm2r = 3 cm (ii) Volume of cylinder =
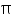 r2h = (3.14
r2h = (3.14  (3)2
(3)2 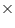 5) cm3 = 141.3 cm3
5) cm3 = 141.3 cm3
Question 5
Assume 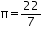 , unless stated otherwise.
, unless stated otherwise.
It costs Rs 2200 to paint the inner curved surface of a cylindrical vessel 10m deep. If the cost of painting is at the rate of Rs 20 per m2, find
(i) Inner curved surface area of the vessel
(ii) Radius of the base
(iii) Capacity of the vessel
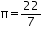 , unless stated otherwise.
, unless stated otherwise. It costs Rs 2200 to paint the inner curved surface of a cylindrical vessel 10m deep. If the cost of painting is at the rate of Rs 20 per m2, find
(i) Inner curved surface area of the vessel
(ii) Radius of the base
(iii) Capacity of the vessel
Solution 5
(i) Cost of painting 1 m2 area = Rs 20
So, Rs 2200 is cost of painting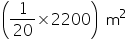 area , i.e, 110 m2 area.
area , i.e, 110 m2 area.
Thus, the inner surface area of the vessel is 110 m2.
(ii) Let radius of base of vessel be r.
Height (h) of vessel = 10 m
Surface area = 2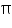 rh = 110 m2
rh = 110 m2
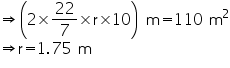 (iii) Capacity of vessel =
(iii) Capacity of vessel = 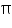 r2h =
r2h =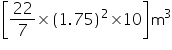 = 96.25 m3
= 96.25 m3
So, Rs 2200 is cost of painting
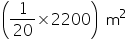 area , i.e, 110 m2 area.
area , i.e, 110 m2 area.Thus, the inner surface area of the vessel is 110 m2.
(ii) Let radius of base of vessel be r.
Height (h) of vessel = 10 m
Surface area = 2
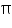 rh = 110 m2
rh = 110 m2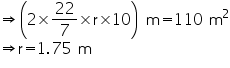 (iii) Capacity of vessel =
(iii) Capacity of vessel = 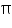 r2h =
r2h =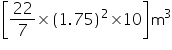 = 96.25 m3
= 96.25 m3
Question 6
Assume 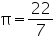 , unless stated otherwise. The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square metres of metal sheet would be needed to make it?
, unless stated otherwise. The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square metres of metal sheet would be needed to make it?
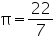 , unless stated otherwise. The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square metres of metal sheet would be needed to make it?
, unless stated otherwise. The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square metres of metal sheet would be needed to make it?
Solution 6
Let radius of the circular ends of the cylinder be r.
Height (h) of the cylindrical vessel = 1 m
Volume of cylindrical vessel = 15.4 litres = 0.0154 m3 Total Surface area of vessel = 2
Total Surface area of vessel = 2 r(r+h)
r(r+h)  Thus, 0.4708 m2 of metal sheet would be needed to make the cylindrical vessel.
Thus, 0.4708 m2 of metal sheet would be needed to make the cylindrical vessel.
Height (h) of the cylindrical vessel = 1 m
Volume of cylindrical vessel = 15.4 litres = 0.0154 m3
 Total Surface area of vessel = 2
Total Surface area of vessel = 2 r(r+h)
r(r+h)  Thus, 0.4708 m2 of metal sheet would be needed to make the cylindrical vessel.
Thus, 0.4708 m2 of metal sheet would be needed to make the cylindrical vessel.
Question 7
Assume  , unless stated otherwise. A lead pencil consists of a cylinder of wood with solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
, unless stated otherwise. A lead pencil consists of a cylinder of wood with solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
 , unless stated otherwise. A lead pencil consists of a cylinder of wood with solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
, unless stated otherwise. A lead pencil consists of a cylinder of wood with solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
Solution 7
Radius (r1) of pencil = 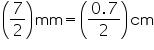 = 0.35 cm
= 0.35 cm
Radius (r2) of graphite =
Height (h) of pencil = 14 cm
Volume of wood in pencil =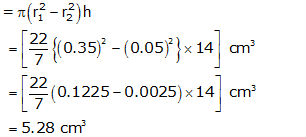 Volume of Graphite =
Volume of Graphite = 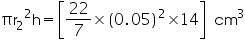 = 0.11 cm3
= 0.11 cm3
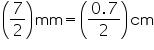 = 0.35 cm
= 0.35 cmRadius (r2) of graphite =
Height (h) of pencil = 14 cm
Volume of wood in pencil =
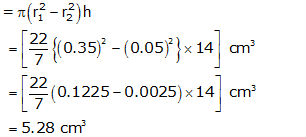 Volume of Graphite =
Volume of Graphite = 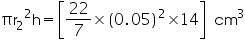 = 0.11 cm3
= 0.11 cm3
Question 8
Assume 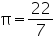 , unless stated otherwise. A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
, unless stated otherwise. A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
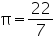 , unless stated otherwise. A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
, unless stated otherwise. A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
Solution 8
Radius (r) of cylindrical bowl = 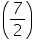 cm = 3.5 cm
cm = 3.5 cm
Height (h) up to which the bowl is filled with soup = 4 cm Volume of soup in 1 bowl =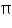 r2h=
r2h= 
Volume of soup in 250 bowls = (250 154) cm3 = 38500 cm3 = 38.5 litres
154) cm3 = 38500 cm3 = 38.5 litres
Thus, the hospital will have to prepare 38.5 litres of soup daily to serve 250 patients.
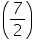 cm = 3.5 cm
cm = 3.5 cmHeight (h) up to which the bowl is filled with soup = 4 cm Volume of soup in 1 bowl =
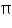 r2h=
r2h= 
Volume of soup in 250 bowls = (250
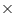 154) cm3 = 38500 cm3 = 38.5 litres
154) cm3 = 38500 cm3 = 38.5 litresThus, the hospital will have to prepare 38.5 litres of soup daily to serve 250 patients.
NCERT Solution for Class 9 Mathematics Chapter 13 - Surface Areas and Volumes Page/Excercise 13.7
Question 1
Assume 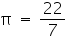 , unless stated otherwise. Find the volume of the right circular cone with
, unless stated otherwise. Find the volume of the right circular cone with
(i) radius 6 cm, height 7 cm
(ii) radius 3.5 cm, height 12 cm
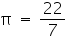 , unless stated otherwise. Find the volume of the right circular cone with
, unless stated otherwise. Find the volume of the right circular cone with(i) radius 6 cm, height 7 cm
(ii) radius 3.5 cm, height 12 cm
Solution 1
(i) Radius (r) of cone = 6 cm
Height (h) of cone = 7 cm
Volume of cone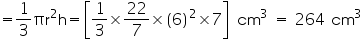
(ii) Radius (r) of cone = 3.5 cm
Height (h) of cone = 12 cm
Volume of cone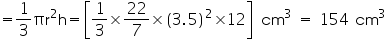
Height (h) of cone = 7 cm
Volume of cone
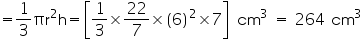
(ii) Radius (r) of cone = 3.5 cm
Height (h) of cone = 12 cm
Volume of cone
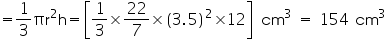
Question 2
Assume 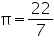 , unless stated otherwise Find the capacity in litres of a conical vessel with
, unless stated otherwise Find the capacity in litres of a conical vessel with
(i) radius 7 cm, slant height 25 cm
(ii) height 12 cm, slant height 13 cm
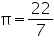 , unless stated otherwise Find the capacity in litres of a conical vessel with
, unless stated otherwise Find the capacity in litres of a conical vessel with(i) radius 7 cm, slant height 25 cm
(ii) height 12 cm, slant height 13 cm
Solution 2
(i) Radius (r) of cone = 7 cm
Slant height (l) of cone = 25 cm
Height (h) of cone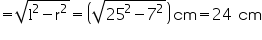
Volume of cone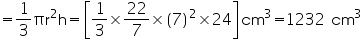
Capacity of the conical vessel =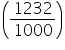 litres= 1.232 litres (ii) Height (h) of cone = 12 cm
litres= 1.232 litres (ii) Height (h) of cone = 12 cm
Slant height (l) of cone = 13 cm
Radius (r) of cone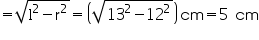
Volume of cone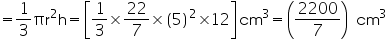
Capacity of the conical vessel =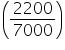 litres =
litres = 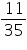 litres.
litres.
Slant height (l) of cone = 25 cm
Height (h) of cone
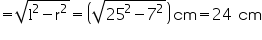
Volume of cone
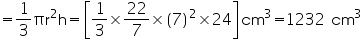
Capacity of the conical vessel =
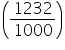 litres= 1.232 litres (ii) Height (h) of cone = 12 cm
litres= 1.232 litres (ii) Height (h) of cone = 12 cmSlant height (l) of cone = 13 cm
Radius (r) of cone
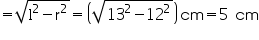
Volume of cone
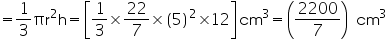
Capacity of the conical vessel =
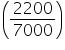 litres =
litres = 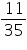 litres.
litres.
Question 3
The height of a cone is 15 cm. If its volume is 1570 cm3, find the diameter of its base. (Use 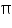 = 3.14)
= 3.14)
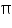 = 3.14)
= 3.14)
Solution 3
Height (h) of cone = 15 cm
Let radius of cone be r.
Volume of cone = 1570 cm3
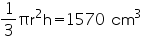
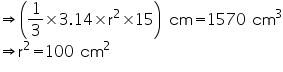 r = 10 cm
r = 10 cm
Thus, the radius of the base of the cone is 10 cm.
Let radius of cone be r.
Volume of cone = 1570 cm3
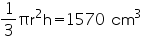
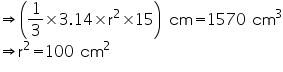 r = 10 cm
r = 10 cmThus, the radius of the base of the cone is 10 cm.
Question 4
Assume 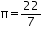 , unless stated otherwise.
, unless stated otherwise.
If the volume of a right circular cone of height 9 cm is 48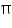 cm3, find the diameter of its base.
cm3, find the diameter of its base.
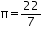 , unless stated otherwise.
, unless stated otherwise. If the volume of a right circular cone of height 9 cm is 48
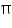 cm3, find the diameter of its base.
cm3, find the diameter of its base.
Solution 4
Height (h) of cone = 9 cm
Let radius of cone be r.
Volume of cone = 48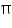 cm3
cm3 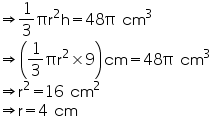
Thus, the diameter of the base of the cone is 2r = 8 cm.
Let radius of cone be r.
Volume of cone = 48
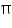 cm3
cm3 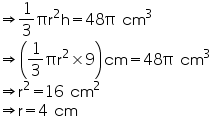
Thus, the diameter of the base of the cone is 2r = 8 cm.
Question 5
Assume 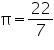 , unless stated otherwise A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?
, unless stated otherwise A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?
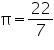 , unless stated otherwise A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?
, unless stated otherwise A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?
Solution 5
Radius (r) of pit =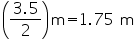
Depth (h) of pit = 12 m
Volume of pit =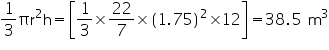 = 38.5 m3
= 38.5 m3  Capacity of the pit = (38.5
Capacity of the pit = (38.5  1) kilolitres = 38.5 kilolitres
1) kilolitres = 38.5 kilolitres
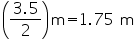
Depth (h) of pit = 12 m
Volume of pit =
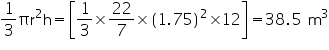 = 38.5 m3
= 38.5 m3  1) kilolitres = 38.5 kilolitres
1) kilolitres = 38.5 kilolitres
Question 6
Assume  , unless stated otherwise.
, unless stated otherwise.
The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find
(i) height of the cone
(ii) slant height of the cone
(iii) curved surface area of the cone
 , unless stated otherwise.
, unless stated otherwise.The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find
(i) height of the cone
(ii) slant height of the cone
(iii) curved surface area of the cone
Solution 6
(i) Radius of cone = 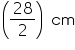 =14 cm
=14 cm
Let height of cone be h.
Volume of cone = 9856 cm3
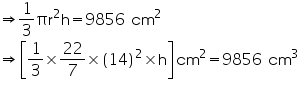 h = 48 cm Thus, the height of the cone is 48 cm. (ii) Slant height (l) of cone
h = 48 cm Thus, the height of the cone is 48 cm. (ii) Slant height (l) of cone 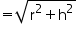

Thus, the slant height of the cone is 50 cm. (iii) CSA of cone = rl=
rl= 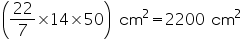 = 2200 cm2
= 2200 cm2
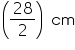 =14 cm
=14 cmLet height of cone be h.
Volume of cone = 9856 cm3
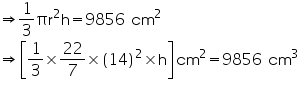 h = 48 cm Thus, the height of the cone is 48 cm. (ii) Slant height (l) of cone
h = 48 cm Thus, the height of the cone is 48 cm. (ii) Slant height (l) of cone 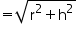

Thus, the slant height of the cone is 50 cm. (iii) CSA of cone =
 rl=
rl= 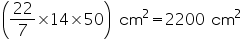 = 2200 cm2
= 2200 cm2
Question 7
Assume  , unless stated otherwise. A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
, unless stated otherwise. A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
 , unless stated otherwise. A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
, unless stated otherwise. A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
Solution 7
When the right angled  ABC is revolved about its side 12 cm, a cone of height (h) 12 cm, radius (r) 5 cm, and slant height (l) 13 cm will be formed.
ABC is revolved about its side 12 cm, a cone of height (h) 12 cm, radius (r) 5 cm, and slant height (l) 13 cm will be formed.
Volume of cone = 100
= 100 cm3
cm3
Thus, the volume of cone so formed by the triangle is 100 cm3.
cm3.
 ABC is revolved about its side 12 cm, a cone of height (h) 12 cm, radius (r) 5 cm, and slant height (l) 13 cm will be formed.
ABC is revolved about its side 12 cm, a cone of height (h) 12 cm, radius (r) 5 cm, and slant height (l) 13 cm will be formed. Volume of cone
 = 100
= 100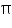 cm3
cm3Thus, the volume of cone so formed by the triangle is 100
 cm3.
cm3.
Question 8
Assume 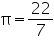 , unless stated otherwise. If the triangle ABC in the Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
, unless stated otherwise. If the triangle ABC in the Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
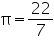 , unless stated otherwise. If the triangle ABC in the Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
, unless stated otherwise. If the triangle ABC in the Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
Solution 8
When the right angled 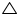 ABC is revolved about its side 5 cm, a cone of radius (r) 12 cm, height (h) 5 cm, and slant height (l) 13 cm will be formed.
ABC is revolved about its side 5 cm, a cone of radius (r) 12 cm, height (h) 5 cm, and slant height (l) 13 cm will be formed.
Volume of cone =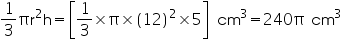 Required ratio
Required ratio 
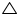 ABC is revolved about its side 5 cm, a cone of radius (r) 12 cm, height (h) 5 cm, and slant height (l) 13 cm will be formed.
ABC is revolved about its side 5 cm, a cone of radius (r) 12 cm, height (h) 5 cm, and slant height (l) 13 cm will be formed.Volume of cone =
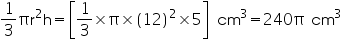 Required ratio
Required ratio 
Question 9
Assume 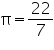 , unless stated otherwise. A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.
, unless stated otherwise. A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.
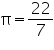 , unless stated otherwise. A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.
, unless stated otherwise. A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.
Solution 9
Radius (r) of heap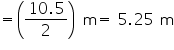
Height (h) of heap = 3 m
Volume of heap=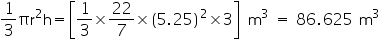
Slant height (l) =
Area of canvas required = CSA of cone
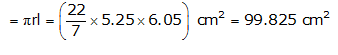
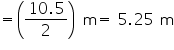
Height (h) of heap = 3 m
Volume of heap=
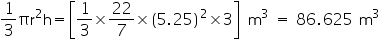
Slant height (l) =

Area of canvas required = CSA of cone
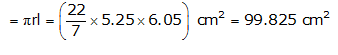
NCERT Solution for Class 9 Mathematics Chapter 13 - Surface Areas and Volumes Page/Excercise 13.8
Question 1
Assume 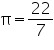 , unless stated otherwise. Find the volume of a sphere whose radius is
, unless stated otherwise. Find the volume of a sphere whose radius is
(i) 7 cm (ii) 0.63 m
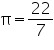 , unless stated otherwise. Find the volume of a sphere whose radius is
, unless stated otherwise. Find the volume of a sphere whose radius is(i) 7 cm (ii) 0.63 m
Solution 1
(i) Radius of sphere = 7 cm
Volume of sphere =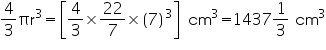 (ii) Radius of sphere = 0.63 m
(ii) Radius of sphere = 0.63 m
Volume of sphere =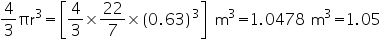 m3(approximately)
m3(approximately)
Volume of sphere =
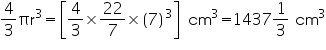 (ii) Radius of sphere = 0.63 m
(ii) Radius of sphere = 0.63 mVolume of sphere =
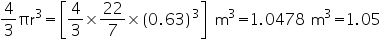 m3(approximately)
m3(approximately)
Question 2
Assume  , unless stated otherwise Find the amount of water displaced by a solid spherical ball of diameter
, unless stated otherwise Find the amount of water displaced by a solid spherical ball of diameter
(i) 28 cm (ii) 0.21 m
 , unless stated otherwise Find the amount of water displaced by a solid spherical ball of diameter
, unless stated otherwise Find the amount of water displaced by a solid spherical ball of diameter(i) 28 cm (ii) 0.21 m
Solution 2
(i) Radius (r) of ball = 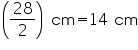
Volume of ball =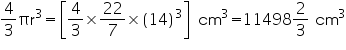
Thus, the amount of water displaced is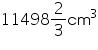 . (ii) Radius (r) of ball =
. (ii) Radius (r) of ball =  = 0.105 m
= 0.105 m
Volume of ball =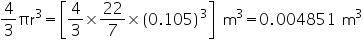
Thus, the amount of water displaced is 0.004851 m3.
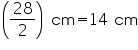
Volume of ball =
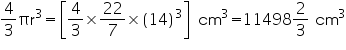
Thus, the amount of water displaced is
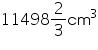 . (ii) Radius (r) of ball =
. (ii) Radius (r) of ball =  = 0.105 m
= 0.105 mVolume of ball =
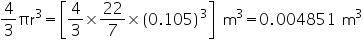
Thus, the amount of water displaced is 0.004851 m3.
Question 3
Assume 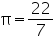 , unless stated otherwise. The diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm3?
, unless stated otherwise. The diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm3?
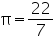 , unless stated otherwise. The diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm3?
, unless stated otherwise. The diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm3?
Solution 3
Radius (r) of metallic ball = 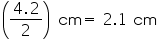
Volume of metallic ball =
Mass = Density Volume = (8.9 * 38.808) g = 345.3912 g
Volume = (8.9 * 38.808) g = 345.3912 g
Thus, the mass of the ball is approximately 345.39 g.
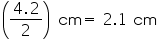
Volume of metallic ball =

Mass = Density
 Volume = (8.9 * 38.808) g = 345.3912 g
Volume = (8.9 * 38.808) g = 345.3912 gThus, the mass of the ball is approximately 345.39 g.
Question 4
Assume 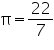 , unless stated otherwise. The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
, unless stated otherwise. The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
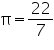 , unless stated otherwise. The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
, unless stated otherwise. The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
Solution 4
Let diameter of earth be d. So, radius earth will be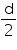 .
.
Then, diameter of moon will be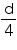 . So, radius of moon will be
. So, radius of moon will be 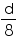 .
.
Volume of moon =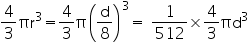
Volume of earth =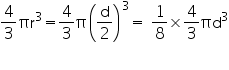
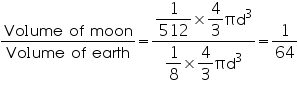
Thus, the volume of moon is of volume of earth.
of volume of earth.
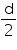 .
.Then, diameter of moon will be
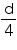 . So, radius of moon will be
. So, radius of moon will be 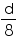 .
.Volume of moon =
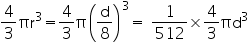
Volume of earth =
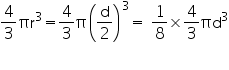
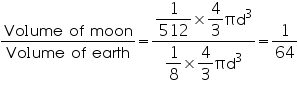
Thus, the volume of moon is
 of volume of earth.
of volume of earth.
Question 5
Assume 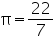 , unless stated otherwise. How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold?
, unless stated otherwise. How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold?
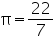 , unless stated otherwise. How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold?
, unless stated otherwise. How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold?
Solution 5
Radius (r) of hemispherical bowl =  = 5.25 cm Volume of hemispherical bowl
= 5.25 cm Volume of hemispherical bowl
= 303.1875 cm3
Capacity of the bowl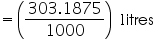
= 0.3031875 litre = 0.303 litre (approximately)
Thus, the hemispherical bowl can hold 0.303 litre of milk.
 = 5.25 cm Volume of hemispherical bowl
= 5.25 cm Volume of hemispherical bowl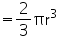
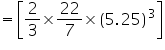
= 303.1875 cm3
Capacity of the bowl
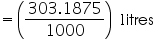
= 0.3031875 litre = 0.303 litre (approximately)
Thus, the hemispherical bowl can hold 0.303 litre of milk.
Question 6
Assume 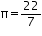 , unless stated otherwise.
, unless stated otherwise.
A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank.
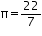 , unless stated otherwise.
, unless stated otherwise.A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank.
Solution 6
Inner radius (r1) of hemispherical tank = 1 m
Thickness of hemispherical tank = 1 cm = 0.01 m
Outer radius (r2) of hemispherical tank = (1 + 0.01) m = 1.01 m Volume of iron used to make the tank =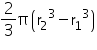

Thickness of hemispherical tank = 1 cm = 0.01 m
Outer radius (r2) of hemispherical tank = (1 + 0.01) m = 1.01 m Volume of iron used to make the tank =
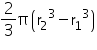

Question 7
Assume 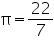 Find the volume of a sphere whose surface area is 154 cm2.
Find the volume of a sphere whose surface area is 154 cm2.
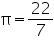 Find the volume of a sphere whose surface area is 154 cm2.
Find the volume of a sphere whose surface area is 154 cm2.
Solution 7
Let the radius of the sphere be r.
Surface area of sphere = 154 cm2
 r2 = 154 cm2
r2 = 154 cm2 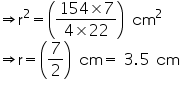
Volume of sphere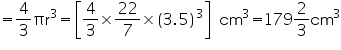
Surface area of sphere = 154 cm2
 r2 = 154 cm2
r2 = 154 cm2 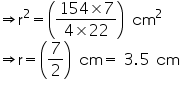
Volume of sphere
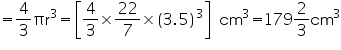
Question 8
Assume 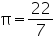 , unless stated otherwise. A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of Rs 498.96. If the cost of white-washing is Rs 2.00 per square meter, find the
, unless stated otherwise. A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of Rs 498.96. If the cost of white-washing is Rs 2.00 per square meter, find the
(i) inside surface area of the dome, (ii) volume of the air inside the dome.
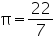 , unless stated otherwise. A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of Rs 498.96. If the cost of white-washing is Rs 2.00 per square meter, find the
, unless stated otherwise. A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of Rs 498.96. If the cost of white-washing is Rs 2.00 per square meter, find the(i) inside surface area of the dome, (ii) volume of the air inside the dome.
Solution 8
(i) Cost of white washing the dome from inside = Rs 498.96
Cost of white washing 1 m2 area = Rs 2
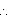 CSA of inner side of dome =
CSA of inner side of dome = 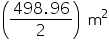 = 249.48 m2 (ii) Let inner radius of hemispherical dome be r.
= 249.48 m2 (ii) Let inner radius of hemispherical dome be r.
CSA of inner side of dome = 249.48 m2
2 r2 = 249.48 m2
r2 = 249.48 m2

Volume of air inside the dome = Volume of the hemispherical dome
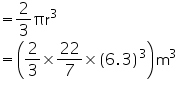
= 523.908 m3
Thus, the volume of air inside the dome is approximately 523.9 m3.
Cost of white washing 1 m2 area = Rs 2
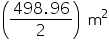 = 249.48 m2 (ii) Let inner radius of hemispherical dome be r.
= 249.48 m2 (ii) Let inner radius of hemispherical dome be r.CSA of inner side of dome = 249.48 m2
2
 r2 = 249.48 m2
r2 = 249.48 m2
Volume of air inside the dome = Volume of the hemispherical dome
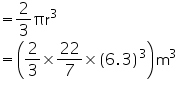
= 523.908 m3
Thus, the volume of air inside the dome is approximately 523.9 m3.
Question 9
Assume 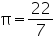 , unless stated otherwise. Twenty seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S'. Find the
, unless stated otherwise. Twenty seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S'. Find the
(i) radius r' of the new sphere, (ii) ratio of S and S'.
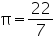 , unless stated otherwise. Twenty seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S'. Find the
, unless stated otherwise. Twenty seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S'. Find the(i) radius r' of the new sphere, (ii) ratio of S and S'.
Solution 9
(i) Radius of 1 solid iron sphere = r
Volume of 1 solid iron sphere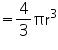
Volume of 27 solid iron spheres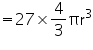
It is given that 27 sold iron spheres are melted to from 1 iron sphere. So, volume of this iron sphere will be equal to volume of 27 solid iron spheres.
Radius of the new sphere = r'.
Volume of new sphere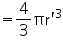
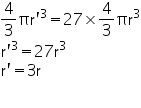 (ii) Surface area of 1 solid iron sphere of radius r = 4
(ii) Surface area of 1 solid iron sphere of radius r = 4 r2
r2
Surface area of iron sphere of radius r' = 4 (r')2 = 4
(r')2 = 4  (3r)2 = 36
(3r)2 = 36  r2
r2
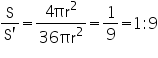
Volume of 1 solid iron sphere
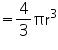
Volume of 27 solid iron spheres
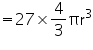
It is given that 27 sold iron spheres are melted to from 1 iron sphere. So, volume of this iron sphere will be equal to volume of 27 solid iron spheres.
Radius of the new sphere = r'.
Volume of new sphere
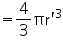
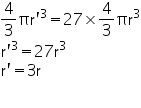 (ii) Surface area of 1 solid iron sphere of radius r = 4
(ii) Surface area of 1 solid iron sphere of radius r = 4 r2
r2Surface area of iron sphere of radius r' = 4
 (r')2 = 4
(r')2 = 4  (3r)2 = 36
(3r)2 = 36  r2
r2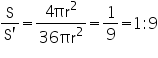
Question 10
Assume  , unless stated otherwise. A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm3) is needed to fill this capsule?
, unless stated otherwise. A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm3) is needed to fill this capsule?
 , unless stated otherwise. A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm3) is needed to fill this capsule?
, unless stated otherwise. A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm3) is needed to fill this capsule?
Solution 10
Radius (r) of capsule
Volume of spherical capsule
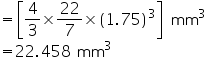
Thus, approximately 22.46 mm3 of medicine is required to fill the capsule.

Volume of spherical capsule

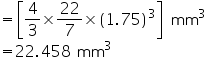
Thus, approximately 22.46 mm3 of medicine is required to fill the capsule.
NCERT Solution for Class 9 Mathematics Chapter 13 - Surface Areas and Volumes Page/Excercise 13.9
Question 1
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm. The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf. 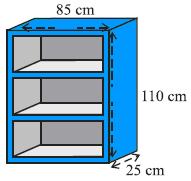

Solution 1
External length (l) of bookshelf = 85 cm
External breadth (b) of bookshelf = 25 cm
External height (h) of bookshelf = 110 cm
External surface area of shelf while leaving front face of shelf
= lh + 2 (lb + bh)
= [85 110 + 2 (85
110 + 2 (85  25 + 25
25 + 25  110)] cm2
110)] cm2
= 19100 cm2
Area of front face = [85 110 - 75
110 - 75  100 + 2 (75
100 + 2 (75  5)] cm2
5)] cm2
= 1850 + 750 cm2
= 2600 cm2
Area to be polished = (19100 + 2600) cm2 = 21700 cm2
Cost of polishing 1 cm2 area = Rs 0.20
Cost of polishing 21700 cm2 area = Rs (21700 0.20) = Rs 4340
0.20) = Rs 4340
Now, length (l), breadth (b) height (h) of each row of bookshelf is 75 cm, 20 cm, and 30cm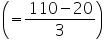 respectively.
respectively.
Area to be painted in 1 row = 2 (l + h) b + lh
= [2 (75 + 30) 20 + 75
20 + 75  30] cm2
30] cm2
= (4200 + 2250) cm2
= 6450 cm2
Area to be painted in 3 rows = (3 6450) cm2 = 19350 cm2
6450) cm2 = 19350 cm2
Cost of painting 1 cm2 area = Rs 0.10
Cost of painting 19350 cm2 area = Rs (19350 0.10) = Rs 1935
0.10) = Rs 1935
Total expense required for polishing and painting the surface of the bookshelf = Rs(4340 + 1935) = Rs 6275
External breadth (b) of bookshelf = 25 cm
External height (h) of bookshelf = 110 cm
External surface area of shelf while leaving front face of shelf
= lh + 2 (lb + bh)
= [85
 110 + 2 (85
110 + 2 (85  25 + 25
25 + 25  110)] cm2
110)] cm2= 19100 cm2
Area of front face = [85
 110 - 75
110 - 75  100 + 2 (75
100 + 2 (75  5)] cm2
5)] cm2= 1850 + 750 cm2
= 2600 cm2
Area to be polished = (19100 + 2600) cm2 = 21700 cm2
Cost of polishing 1 cm2 area = Rs 0.20
Cost of polishing 21700 cm2 area = Rs (21700
 0.20) = Rs 4340
0.20) = Rs 4340 Now, length (l), breadth (b) height (h) of each row of bookshelf is 75 cm, 20 cm, and 30cm
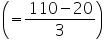 respectively.
respectively.Area to be painted in 1 row = 2 (l + h) b + lh
= [2 (75 + 30)
 20 + 75
20 + 75  30] cm2
30] cm2= (4200 + 2250) cm2
= 6450 cm2
Area to be painted in 3 rows = (3
 6450) cm2 = 19350 cm2
6450) cm2 = 19350 cm2Cost of painting 1 cm2 area = Rs 0.10
Cost of painting 19350 cm2 area = Rs (19350
 0.10) = Rs 1935
0.10) = Rs 1935 Total expense required for polishing and painting the surface of the bookshelf = Rs(4340 + 1935) = Rs 6275
Question 2
The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in the given figure. Eight such spheres are used for this purpose, and are to be painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm2 and black paint costs 5 paise per cm2. 

Solution 2
Radius (r) of a wooden sphere = 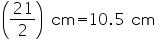 Surface area of a wooden sphere =
Surface area of a wooden sphere = 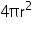 =
=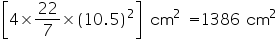
Radius (r') of cylindrical support = 1.5 cm
Height (h) of cylindrical support = 7 cm CSA of cylindrical support = 2 r'h
r'h 
Area of circular end of cylindrical support = r2
r2 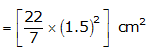 = 7.07 cm2
= 7.07 cm2
Area to be painted silver = [8 (1386 - 7.07)] cm2
(1386 - 7.07)] cm2
= (8 1378.93) cm2 = 11031.44 cm2
1378.93) cm2 = 11031.44 cm2
Cost occurred in painting silver colour = Rs (11031.44 0.25) = Rs 2757.86
0.25) = Rs 2757.86
Area to painted black = (8 66) cm2 = 528 cm2
66) cm2 = 528 cm2
Cost occurred in painting black colour = Rs (528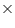 0.05) = Rs 26.40
0.05) = Rs 26.40
 Total cost occurred in painting = Rs (2757.86 + 26.40) = Rs 2784.26
Total cost occurred in painting = Rs (2757.86 + 26.40) = Rs 2784.26
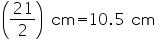 Surface area of a wooden sphere =
Surface area of a wooden sphere =  =
=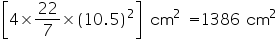
Radius (r') of cylindrical support = 1.5 cm
Height (h) of cylindrical support = 7 cm CSA of cylindrical support = 2
 r'h
r'h Area of circular end of cylindrical support =
 r2
r2  = 7.07 cm2
= 7.07 cm2Area to be painted silver = [8
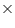 (1386 - 7.07)] cm2
(1386 - 7.07)] cm2= (8
 1378.93) cm2 = 11031.44 cm2
1378.93) cm2 = 11031.44 cm2Cost occurred in painting silver colour = Rs (11031.44
 0.25) = Rs 2757.86
0.25) = Rs 2757.86 Area to painted black = (8
 66) cm2 = 528 cm2
66) cm2 = 528 cm2 Cost occurred in painting black colour = Rs (528
 0.05) = Rs 26.40
0.05) = Rs 26.40
Question 3
The diameter of a sphere is decreased by 25%. By what per cent does its curved surface area decrease?
Solution 3
Let the diameter of the sphere be d.
Radius (r1) of the sphere =
It is given that the diameter of the sphere is decreased by 25%.
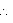 New radus (r2) of the sphere =
New radus (r2) of the sphere = 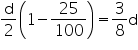 CSA (S1) of the sphere =
CSA (S1) of the sphere = 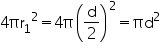
CSA (S2) of the new sphere =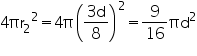
Decrease in CSA of sphere = S1 - S2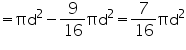
Percentage decrease in CSA of sphere=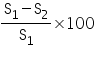
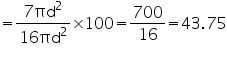 %
%
Radius (r1) of the sphere =

It is given that the diameter of the sphere is decreased by 25%.
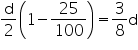 CSA (S1) of the sphere =
CSA (S1) of the sphere = 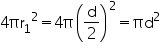
CSA (S2) of the new sphere =
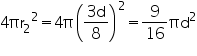
Decrease in CSA of sphere = S1 - S2
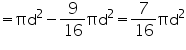
Percentage decrease in CSA of sphere=
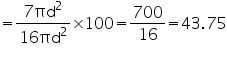 %
%
No comments:
Post a Comment