NCERT Solution for Class 10 Mathematics Chapter 13 - Surface Areas and Volumes
Excercise 13.1
Question 1

Solution 1

Question 2

Solution 2
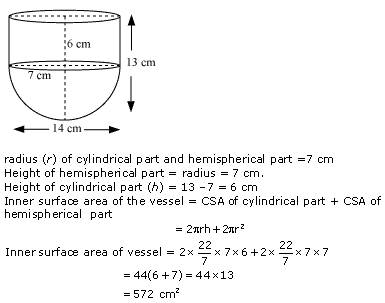
Question 3
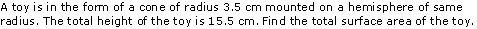
Solution 3
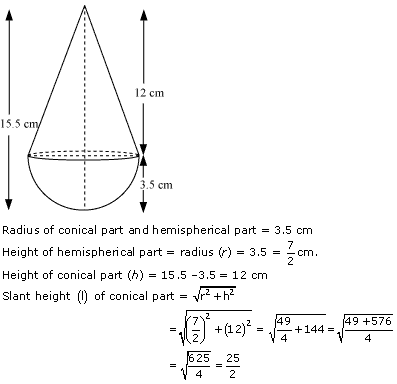

Question 4
Solution 4

Question 5

Solution 5

Question 6
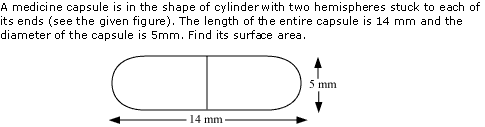

Solution 6
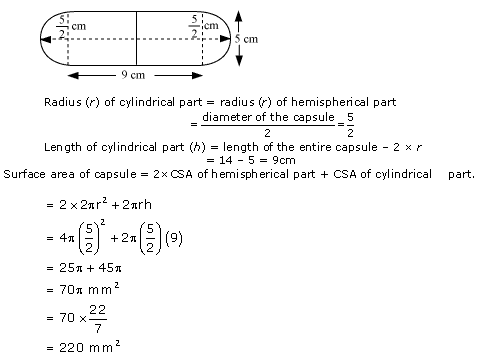
Question 7


Solution 7
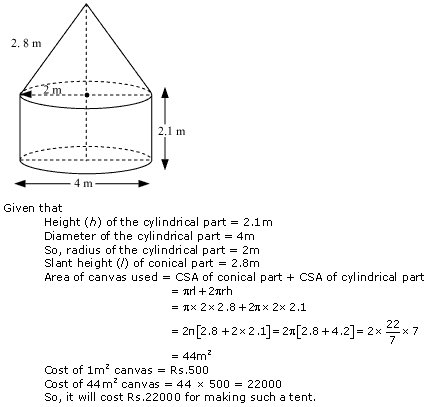
Question 8
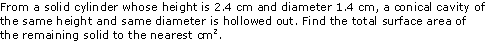
Solution 8

Question 9
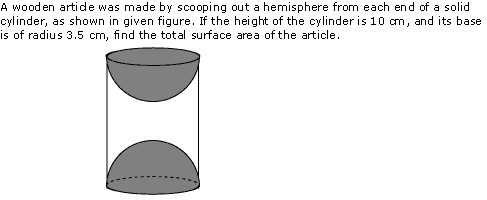

Solution 9

NCERT Solution for Class 10 Mathematics Chapter 13 - Surface Areas and Volumes Page/Excercise 13.2
Question 1
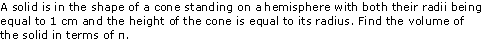
Solution 1
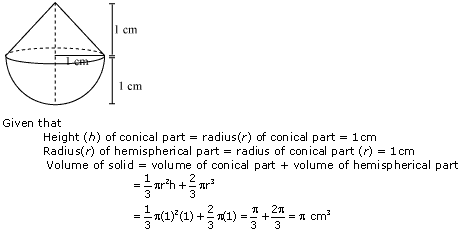
Question 2


Solution 2
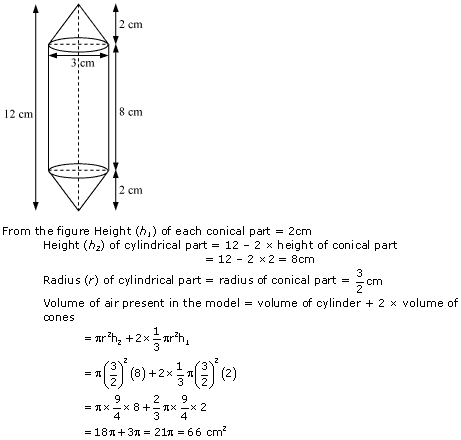
Question 3
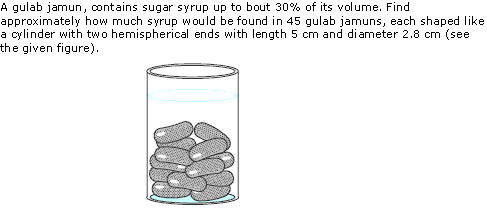
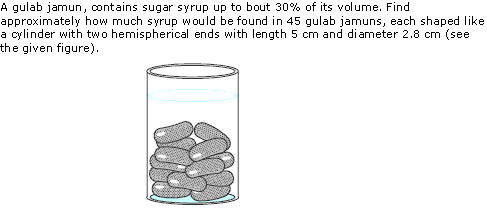
Solution 3

Question 4
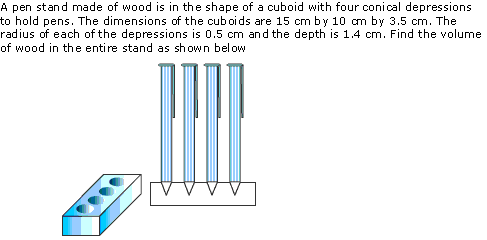

Solution 4
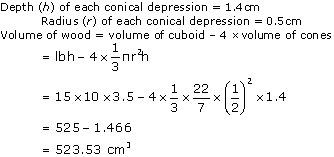
Question 5


Solution 5
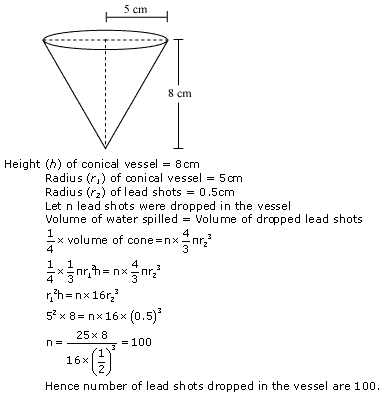
Question 6


Solution 6
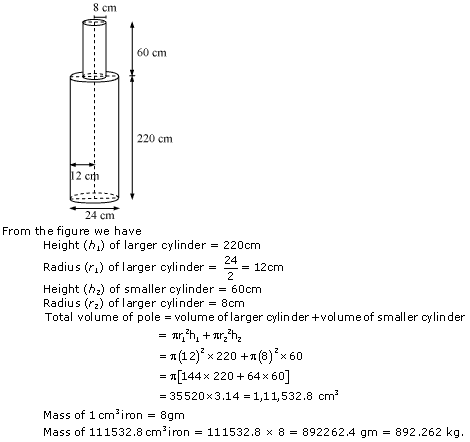
Question 7


Solution 7

Question 8
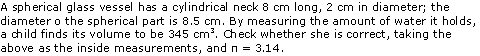
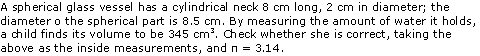
Solution 8
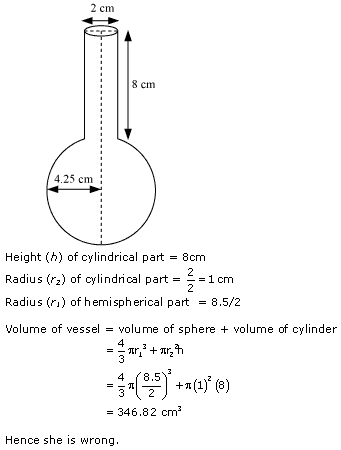
NCERT Solution for Class 10 Mathematics Chapter 13 - Surface Areas and Volumes Page/Excercise 13.3
Question 1

Solution 1

Question 2
Solution 2

Question 3
Solution 3
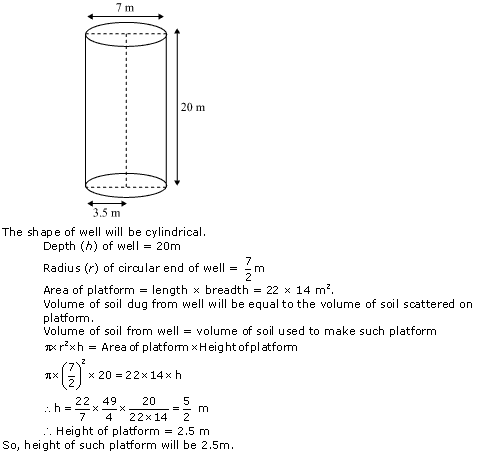
Question 4

Solution 4
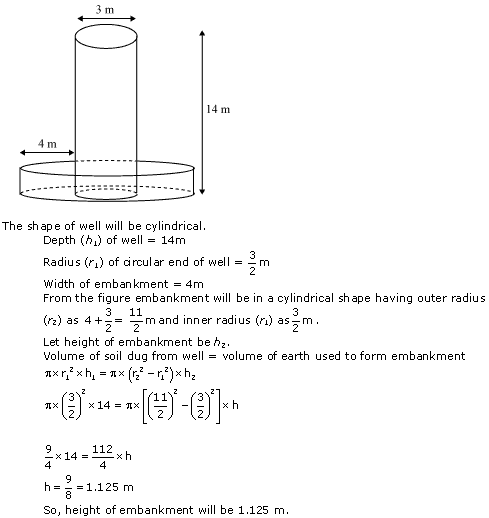
Question 5
A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
Solution 5
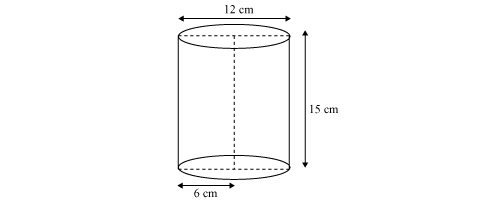

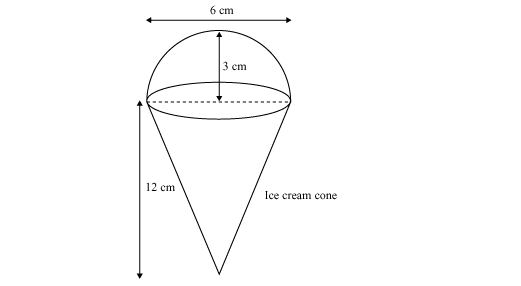

Question 6
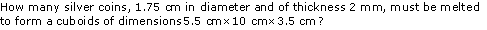
Solution 6

Question 7
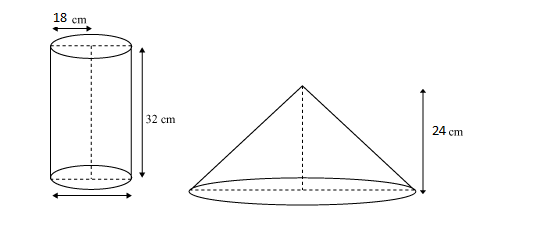
A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm. find the radius and slant height of the heap.
Solution 7

Question 8
Solution 8

Question 9
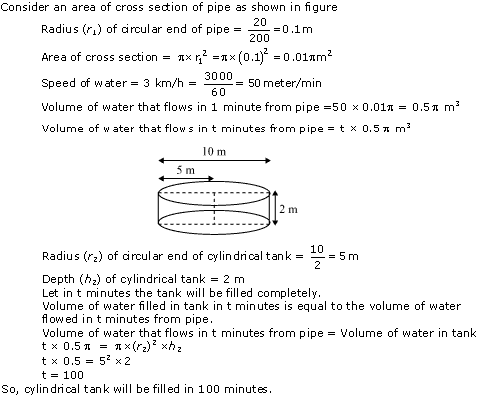
A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
Solution 9
NCERT Solution for Class 10 Mathematics Chapter 13 - Surface Areas and Volumes Page/Excercise 13.4
Question 1

Solution 1
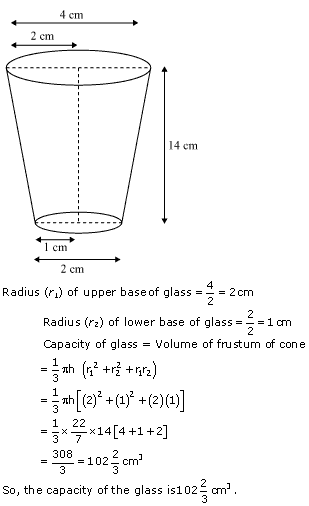
Question 2
Solution 2

Question 3

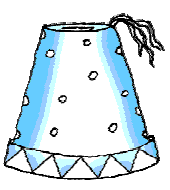

Solution 3
Question 4
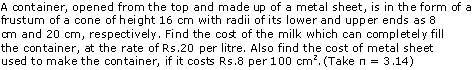
Solution 4

Question 5
Solution 5
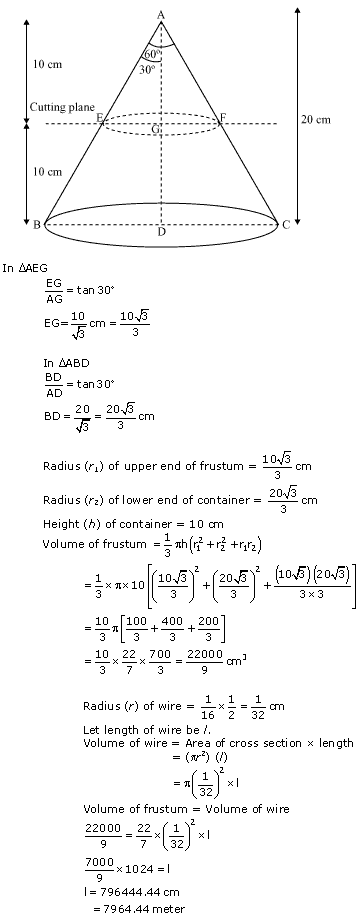
NCERT Solution for Class 10 Mathematics Chapter 13 - Surface Areas and Volumes Page/Excercise 13.5
Question 1

Solution 1

Question 2
A right triangle whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed.
Solution 2
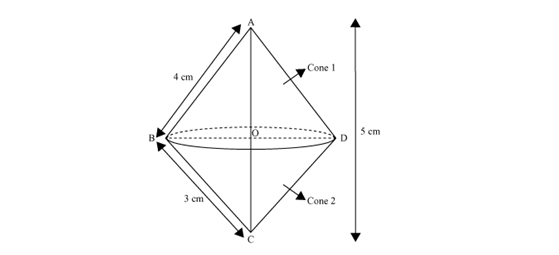

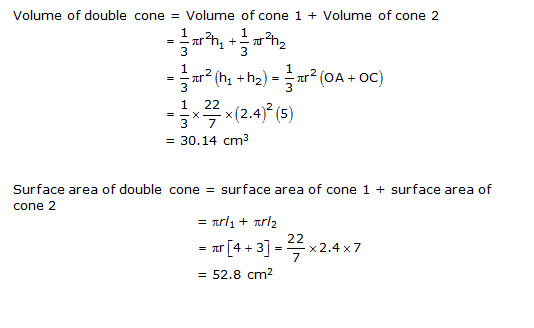
Question 3
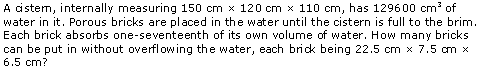
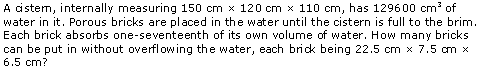
Solution 3

Question 4
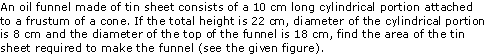
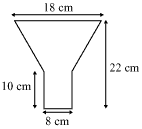
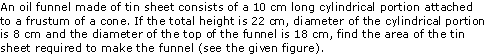

Solution 4
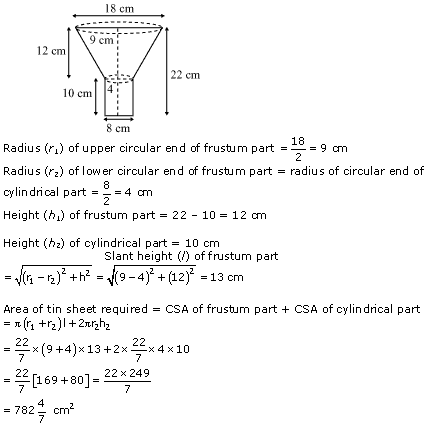
Question 5
Derive the formula for the curved surface area and total surface area of the frustum of cone, using the symbols as explained.
Solution 5
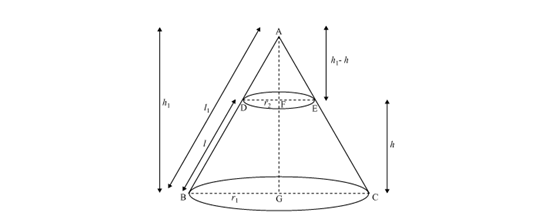

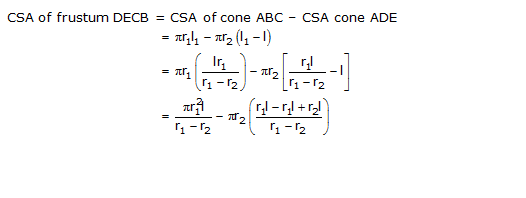

Question 6
Derive the formula for the volume of the frustum of a cone, given to you, using the symbols as explained.
Solution 6
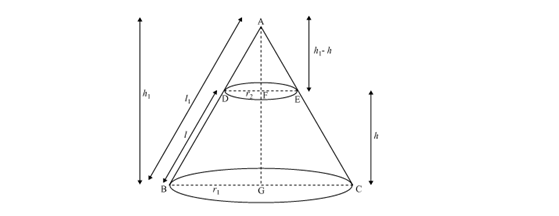

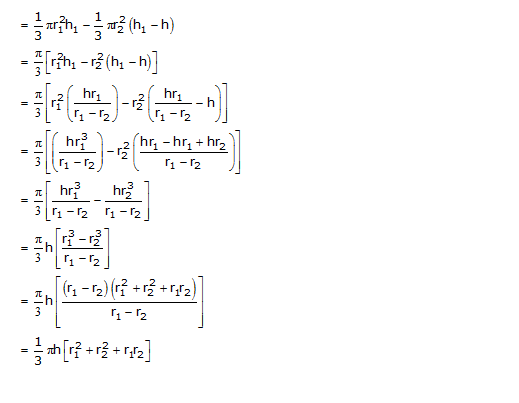
No comments:
Post a Comment