NCERT Solution for Class 9 Mathematics Chapter 10 - Circles Page/Excercise 10.1
Question 1
Fill in the blanks
(i) The centre of a circle lies in __________ of the circle. (exterior/interior)
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
(iii) The longest chord of a circle is a __________ of the circle.
(iv) An arc is a __________ when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and __________ of the circle.
(vi) A circle divides the plane, on which it lies, in __________ parts.
(i) The centre of a circle lies in __________ of the circle. (exterior/interior)
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
(iii) The longest chord of a circle is a __________ of the circle.
(iv) An arc is a __________ when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and __________ of the circle.
(vi) A circle divides the plane, on which it lies, in __________ parts.
Solution 1
(i) The centre of a circle lies in interior of the circle. (exterior/interior)
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in exterior of the circle. (exterior/interior)
(iii) The longest chord of a circle is a diameter of the circle.
(iv) An arc is a semicircle when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and chord of the circle.
(vi) A circle divides the plane, on which it lies, in three parts.
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in exterior of the circle. (exterior/interior)
(iii) The longest chord of a circle is a diameter of the circle.
(iv) An arc is a semicircle when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and chord of the circle.
(vi) A circle divides the plane, on which it lies, in three parts.
Question 2
Write True or False: Give reasons for your answers. (i) Line segment joining the centre of any point on the circle is a radius of the circle.
(ii) A circle has only finite number of equal chords.
(iii) If a circle is divided into three equal arcs, each is a major arc.
(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
(v) Sector is the region between the chord and its corresponding arc.
(vi) A circle is a plane figure.
(ii) A circle has only finite number of equal chords.
(iii) If a circle is divided into three equal arcs, each is a major arc.
(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
(v) Sector is the region between the chord and its corresponding arc.
(vi) A circle is a plane figure.
Solution 2
(i) True, all the points on circle are at equal distance from the centre of circle, and this equal distance it called as radius of circle. (ii) False, on a circle there are infinite points. So, we can draw infinite number of chords of given length. Hence, a circle has infinite number of equal chords. (iii) False, consider three arcs of same length as AB, BC and CA. Now we may observe that for minor arc BDC. CAB is major arc. So AB, BC and CA are minor arcs of circle. 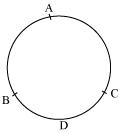 (iv) True, let AB be a chord which is twice as long as its radius. In this situation our chord will be passing through centre of circle. So it will be the diameter of circle.
(iv) True, let AB be a chord which is twice as long as its radius. In this situation our chord will be passing through centre of circle. So it will be the diameter of circle. 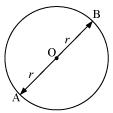 (v) False, sector is the region between an arc and two radii joining the centre to the end points of the arc as in the given figure OAB is the sector of circle.
(v) False, sector is the region between an arc and two radii joining the centre to the end points of the arc as in the given figure OAB is the sector of circle.  (vi) True, A circle is a two dimensional figure and it can also be referred as plane figure.
(vi) True, A circle is a two dimensional figure and it can also be referred as plane figure.
 (iv) True, let AB be a chord which is twice as long as its radius. In this situation our chord will be passing through centre of circle. So it will be the diameter of circle.
(iv) True, let AB be a chord which is twice as long as its radius. In this situation our chord will be passing through centre of circle. So it will be the diameter of circle.  (v) False, sector is the region between an arc and two radii joining the centre to the end points of the arc as in the given figure OAB is the sector of circle.
(v) False, sector is the region between an arc and two radii joining the centre to the end points of the arc as in the given figure OAB is the sector of circle.  (vi) True, A circle is a two dimensional figure and it can also be referred as plane figure.
(vi) True, A circle is a two dimensional figure and it can also be referred as plane figure.NCERT Solution for Class 9 Mathematics Chapter 10 - Circles Page/Excercise 10.2
Question 1
Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Solution 1
A circle is a collection of points which are equidistant from a fix point. This fix point is called as the centre of circle and this equal distance is called as radius of circle. And thus shape of a circle depends on the radius of the circle.
So, if we try to superimpose two circles of equal radius, one each other both circles will cover each other.
So, two circles are congruent if they have equal radius. Now consider two congruent circles having centre O and O' and two chords AB and CD of equal lengths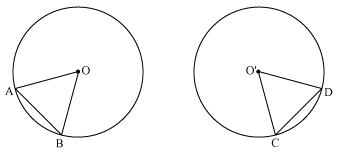 Now in
Now in  AOB and
AOB and  CO'D
CO'D
AB = CD (chords of same length)
OA = O'C (radii of congruent circles)
OB = O'D (radii of congruent circles)
 AOB
AOB 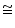
 CO'D (SSS congruence rule)
CO'D (SSS congruence rule)
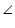 AOB =
AOB = 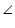 CO'D (by CPCT)
CO'D (by CPCT)
Hence equal chords of congruent circles subtend equal angles at their centres.
So, if we try to superimpose two circles of equal radius, one each other both circles will cover each other.
So, two circles are congruent if they have equal radius. Now consider two congruent circles having centre O and O' and two chords AB and CD of equal lengths
 Now in
Now in  AOB and
AOB and  CO'D
CO'DAB = CD (chords of same length)
OA = O'C (radii of congruent circles)
OB = O'D (radii of congruent circles)
 AOB
AOB 
 CO'D (SSS congruence rule)
CO'D (SSS congruence rule) 
 AOB =
AOB =  CO'D (by CPCT)
CO'D (by CPCT) Hence equal chords of congruent circles subtend equal angles at their centres.
Question 2
Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Solution 2
Let us consider two congruent circles (circles of same radius) with centres as O and O'. 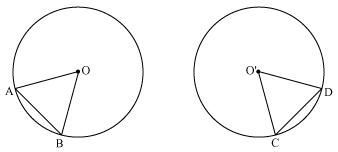 In
In 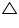 AOB and
AOB and  CO'D
CO'D
 AOB =
AOB =  CO'D (given)
CO'D (given)
OA = O'C (radii of congruent circles)
OB = O'D (radii of congruent circles)
 AOB
AOB  CO'D (SSS congruence rule)
CO'D (SSS congruence rule)
 AB = CD (by CPCT)
AB = CD (by CPCT)
Hence, if chords of congruent circles subtend equal angles at their centres then chords are equal.
 In
In 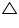 AOB and
AOB and 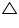 CO'D
CO'D AOB =
AOB =  CO'D (given)
CO'D (given) OA = O'C (radii of congruent circles)
OB = O'D (radii of congruent circles)
 AOB
AOB  CO'D (SSS congruence rule)
CO'D (SSS congruence rule)  AB = CD (by CPCT)
AB = CD (by CPCT) Hence, if chords of congruent circles subtend equal angles at their centres then chords are equal.
NCERT Solution for Class 9 Mathematics Chapter 10 - Circles Page/Excercise 10.3
Question 1
Draw different pair of circles. How many points does each pair have in common? What is the maximum number of common points?
Solution 1
Consider the following pair of circles.
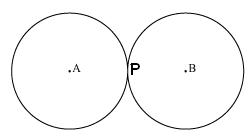
(i) circles don't intersect each other at any point, so circles are not having any point in common.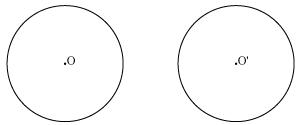 (ii) Circles touch each other only at one point P so there is only 1 point in common.
(ii) Circles touch each other only at one point P so there is only 1 point in common.
 (iii) Circles touch each other at 1 point X only. So the circles have 1 point in common.
(iii) Circles touch each other at 1 point X only. So the circles have 1 point in common.
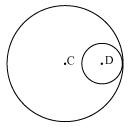
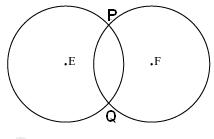
(iv) These circles intersect each other at two points P and Q. So the circles have two points in common. We may observe that there can be maximum 2 points in common.
We can have a situation in which two congruent circles are superimposed on each other, this situation can be referred as if we are drawing circle two times.
(i) circles don't intersect each other at any point, so circles are not having any point in common.
 (ii) Circles touch each other only at one point P so there is only 1 point in common.
(ii) Circles touch each other only at one point P so there is only 1 point in common. (iii) Circles touch each other at 1 point X only. So the circles have 1 point in common.
(iii) Circles touch each other at 1 point X only. So the circles have 1 point in common. 
(iv) These circles intersect each other at two points P and Q. So the circles have two points in common. We may observe that there can be maximum 2 points in common.

We can have a situation in which two congruent circles are superimposed on each other, this situation can be referred as if we are drawing circle two times.
Question 2
Suppose you are given a circle, Give a construction to find its centre.
Solution 2
Following are the steps of construction:
Step1. Take the given circle centered at point O.
Step2. Take any two different chords AB and CD of this circle and draw perpendicular bisectors of these chords.
Step3. Let these perpendicular bisectors meet at point O. Now, O is the centre of given circle.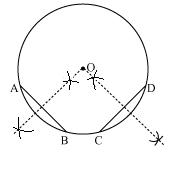
Step1. Take the given circle centered at point O.
Step2. Take any two different chords AB and CD of this circle and draw perpendicular bisectors of these chords.
Step3. Let these perpendicular bisectors meet at point O. Now, O is the centre of given circle.

Question 3
If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord. 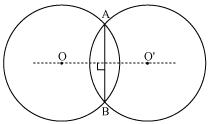

Solution 3
Consider two circles centered at point O and O' intersect each other at point A and B respectively.
Join AB. AB is the chord for circle centered at O, so perpendicular bisector of AB will pass through O.
Again AB is also chord of circle centered at O', so, perpendicular bisector of AB will also pass through O'.
Clearly centres of these circles lie on the perpendicular bisector of common chord.
Join AB. AB is the chord for circle centered at O, so perpendicular bisector of AB will pass through O.
Again AB is also chord of circle centered at O', so, perpendicular bisector of AB will also pass through O'.
Clearly centres of these circles lie on the perpendicular bisector of common chord.
NCERT Solution for Class 9 Mathematics Chapter 10 - Circles Page/Excercise 10.4
Question 1
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Solution 1

Let radius of circle centered at O and O' be 5 cm and 3 cm respectively.
OA = OB = 5 cm
O'A = O'B = 3 cm
OO' will be the perpendicular bisector of chord AB.
Given that OO' = 4 cm
Let OC be x. so, O'C will be 4 - x
In
 OAC
OACOA2 = AC2 + OC2
 52 = AC2 + x2
52 = AC2 + x2 25 - x2 = AC2 ... (1)
25 - x2 = AC2 ... (1) In
 O'AC
O'ACO'A2 = AC2 + O'C2
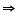 32 = AC2 + (4 - x)2
32 = AC2 + (4 - x)2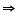 9 = AC2 + 16 + x2 - 8x
9 = AC2 + 16 + x2 - 8x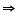 AC2 = - x2 - 7 + 8x ... (2)
AC2 = - x2 - 7 + 8x ... (2) From equations (1) and (2), we have
25 - x2 = - x2 - 7 + 8x
8x = 32
x = 4
So, the common chord will pass through the centre of smaller circle i.e. O'. and hence it will be diameter of smaller circle.
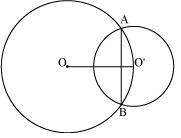 Now, AC2 = 25 - x2 = 25 - 42 = 25 - 16 = 9
Now, AC2 = 25 - x2 = 25 - 42 = 25 - 16 = 9The length of the common chord AB = 2 AC = (2
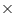 3) m = 6 m
3) m = 6 m
Question 2
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Solution 2
Let PQ and RS are two equal chords of a given circle and there are intersecting each other at point T.  Draw perpendiculars OV and OU on these chords.
Draw perpendiculars OV and OU on these chords.
In OVT and
OVT and  OUT
OUT
OV = OU (Equal chords of a circle are equidistant from the centre)
 OVT =
OVT =  OUT (Each 90o)
OUT (Each 90o)
OT = OT (common)
 OVT
OVT 
 OUT (RHS congruence rule)
OUT (RHS congruence rule)  VT = UT (by CPCT) ... (1)
VT = UT (by CPCT) ... (1)
It is given that
PQ = RS ... ... ... ... (2)
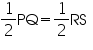
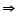 PV = RU ... ... ... ... (3)
PV = RU ... ... ... ... (3)
On adding equations (1) and (3), we have
PV + VT = RU + UT
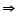 PT = RT ... ... ... ... (4)
PT = RT ... ... ... ... (4)
On subtracting equation (4) from equation (2), we have
PQ - PT = RS - RT
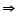 QT = ST ... ... ... ... (5)
QT = ST ... ... ... ... (5)
Equations (4) and (5) shows that the corresponding segments of
chords PQ and RS are congruent to each other.
 Draw perpendiculars OV and OU on these chords.
Draw perpendiculars OV and OU on these chords.In
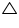 OVT and
OVT and 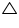 OUT
OUTOV = OU (Equal chords of a circle are equidistant from the centre)
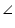 OVT =
OVT = 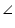 OUT (Each 90o)
OUT (Each 90o)OT = OT (common)
 OVT
OVT 
 OUT (RHS congruence rule)
OUT (RHS congruence rule) It is given that
PQ = RS ... ... ... ... (2)
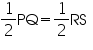
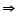 PV = RU ... ... ... ... (3)
PV = RU ... ... ... ... (3) On adding equations (1) and (3), we have
PV + VT = RU + UT
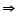 PT = RT ... ... ... ... (4)
PT = RT ... ... ... ... (4)On subtracting equation (4) from equation (2), we have
PQ - PT = RS - RT
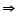 QT = ST ... ... ... ... (5)
QT = ST ... ... ... ... (5) Equations (4) and (5) shows that the corresponding segments of
chords PQ and RS are congruent to each other.
Question 3
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Solution 3
 Let PQ and RS are two equal chords of a given circle and there are intersecting each other at point T.
Let PQ and RS are two equal chords of a given circle and there are intersecting each other at point T.Draw perpendiculars OV and OU on these chords.
In
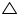 OVT and
OVT and 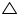 OUT
OUTOV = OU (Equal chords of a circle are equidistant from the centre)
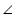 OVT =
OVT = 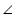 OUT (Each 90o)
OUT (Each 90o)OT = OT (common)
 OVT
OVT  OUT (RHS congruence rule)
OUT (RHS congruence rule)  OTV =
OTV =  OTU (by CPCT) Hence, the line joining the point of intersection to the centre makes equal angles with the chords.
OTU (by CPCT) Hence, the line joining the point of intersection to the centre makes equal angles with the chords.
Question 4
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD. 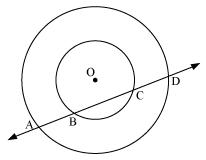

Solution 4
Let us draw a perpendicular OM on line AD.
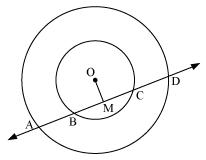
Here, BC is chord of smaller circle and AD is chord of bigger circle.
We know that the perpendicular drawn from centre of circle bisects the chord.
 BM = MC ... (1)
BM = MC ... (1)
And AM = MD ... (2)
Subtracting equations (2) from (1), we have
AM - BM = MD - MC
 AB = CD
AB = CD

Here, BC is chord of smaller circle and AD is chord of bigger circle.
We know that the perpendicular drawn from centre of circle bisects the chord.
And AM = MD ... (2)
Subtracting equations (2) from (1), we have
AM - BM = MD - MC
 AB = CD
AB = CD
Question 5
Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip?
Solution 5
Draw perpendiculars OA and OB on RS and SM respectively.
Let R, S and M be the position of Reshma, Salma and Mandip respectively.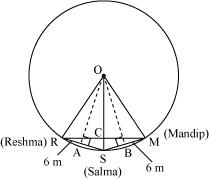 AR = AS =
AR = AS = 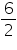 = 3cm OR = OS = OM = 5 m (radii of circle)
= 3cm OR = OS = OM = 5 m (radii of circle)
In OAR
OA2 + AR2 = OR2
OA2 + (3 m)2 = (5 m)2
OA2 = (25 - 9) m2 = 16 m2
OA = 4 m
We know that in an isosceles triangle altitude divides the base, so in RSM
RSM
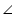 RCS will be of 90o and RC = CM
RCS will be of 90o and RC = CM
Area of ORS =
ORS = 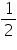
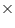 OA
OA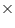 RS
RS 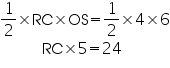
RC = 4.8 RM = 2RC = 2(4.8)= 9.6 So, distance between Reshma and Mandip is 9.6 m.
Let R, S and M be the position of Reshma, Salma and Mandip respectively.
 AR = AS =
AR = AS = 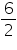 = 3cm OR = OS = OM = 5 m (radii of circle)
= 3cm OR = OS = OM = 5 m (radii of circle)In OAR
OA2 + AR2 = OR2
OA2 + (3 m)2 = (5 m)2
OA2 = (25 - 9) m2 = 16 m2
OA = 4 m
We know that in an isosceles triangle altitude divides the base, so in
 RSM
RSM RCS will be of 90o and RC = CM
RCS will be of 90o and RC = CM Area of
 ORS =
ORS = 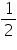
 OA
OA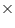 RS
RS 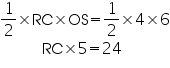
RC = 4.8 RM = 2RC = 2(4.8)= 9.6 So, distance between Reshma and Mandip is 9.6 m.
Question 6
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Solution 6
 Given that AS = SD = DA
Given that AS = SD = DASo, ASD is a equilateral triangle
OA (radius) = 20 m.
Medians of equilateral triangle pass through the circum centre (O) of the equilateral triangle ABC.
We also know that median intersect each other at the 2: 1. As AB is the median of equilateral triangle ABC, we can write
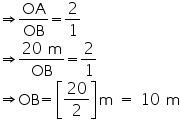
In
 ABD
ABDAD2 = AB2 + BD2
AD2 = (30)2 +
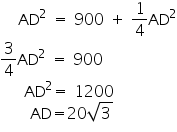
So, length of string of each phone will be
NCERT Solution for Class 9 Mathematics Chapter 10 - Circles Page/Excercise 10.5
Question 1
In the given figure, A, B and C are three points on a circle with centre O such that  BOC = 30o and
BOC = 30o and  AOB = 60o. If D is a point on the circle other than the arc ABC, find
AOB = 60o. If D is a point on the circle other than the arc ABC, find  ADC.
ADC. 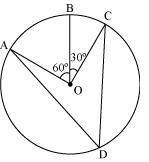
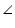 BOC = 30o and
BOC = 30o and 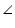 AOB = 60o. If D is a point on the circle other than the arc ABC, find
AOB = 60o. If D is a point on the circle other than the arc ABC, find 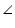 ADC.
ADC. 
Solution 1
We may observe that
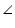 AOC =
AOC =  AOB +
AOB +  BOC
BOC
= 60o + 30o
= 90o
We know that angle subtended by an arc at centre is double the angle subtended by it any point on the remaining part of the circle.
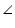 AOC =
AOC =  AOB +
AOB +  BOC
BOC= 60o + 30o
= 90o
We know that angle subtended by an arc at centre is double the angle subtended by it any point on the remaining part of the circle.
Question 2
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Solution 2
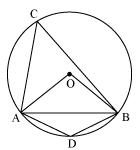 In
In  OAB
OABAB = OA = OB = radius
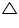 OAB is an equilateral triangle.
OAB is an equilateral triangle. So, each interior angle of this triangle will be of 60o
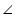 AOB = 60o Now,
AOB = 60o Now, 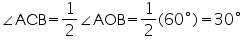 In cyclic quadrilateral ACBD
In cyclic quadrilateral ACBD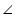 ACB +
ACB + 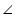 ADB = 180o (Opposite angle in cyclic quadrilateral)
ADB = 180o (Opposite angle in cyclic quadrilateral) ADB = 180o - 30o = 150o
ADB = 180o - 30o = 150o So, angle subtended by this chord at a point on major arc and minor arc are 30o and 150o respectively.
Question 3
In the given figure, 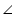 PQR = 100o, where P, Q and R are points on a circle with centre O. Find
PQR = 100o, where P, Q and R are points on a circle with centre O. Find 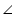 OPR.
OPR. 
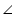 PQR = 100o, where P, Q and R are points on a circle with centre O. Find
PQR = 100o, where P, Q and R are points on a circle with centre O. Find 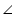 OPR.
OPR. 
Solution 3

Consider PR as a chord of circle.
Take any point S on major arc of circle.
Now PQRS is a cyclic quadrilateral.
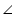 PQR +
PQR + 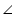 PSR = 180o (Opposite angles of cyclic quadrilateral)
PSR = 180o (Opposite angles of cyclic quadrilateral) 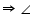 PSR = 180o - 100o = 80o
PSR = 180o - 100o = 80oWe know that angle subtended by an arc at centre is double the angle subtended by it any point on the remaining part of the circle.
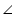 POR = 2
POR = 2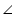 PSR = 2 (80o) = 160o In
PSR = 2 (80o) = 160o In 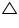 POR
POROP = OR (radii of same circle)
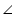 OPR =
OPR = 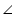 ORP (Angles opposite equal sides of a triangle)
ORP (Angles opposite equal sides of a triangle) 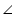 OPR +
OPR + 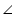 ORP +
ORP + 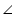 POR = 180o (Angle sum property of a triangle) 2
POR = 180o (Angle sum property of a triangle) 2  OPR + 160o= 180o
OPR + 160o= 180o2
 OPR = 180o - 160o = 20o
OPR = 180o - 160o = 20o  OPR = 10o
OPR = 10o
Question 4
In the given figure,  ABC = 69o,
ABC = 69o, 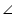 ACB = 31o, find
ACB = 31o, find  BDC.
BDC. 
 ABC = 69o,
ABC = 69o, 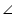 ACB = 31o, find
ACB = 31o, find 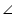 BDC.
BDC. 
Solution 4
In 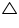 ABC
ABC 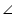 BAC +
BAC + 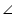 ABC +
ABC + 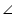 ACB = 180o (Angle sum property of a triangle)
ACB = 180o (Angle sum property of a triangle)
 BAC + 69o + 31o = 180o
BAC + 69o + 31o = 180o  BAC = 180o - 100º
BAC = 180o - 100º
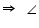 BAC = 80o
BAC = 80o 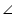 BDC =
BDC = 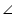 BAC = 80o (Angles in same segment of circle are equal)
BAC = 80o (Angles in same segment of circle are equal)
 ABC
ABC  BAC +
BAC +  ABC +
ABC +  ACB = 180o (Angle sum property of a triangle)
ACB = 180o (Angle sum property of a triangle) 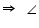 BAC + 69o + 31o = 180o
BAC + 69o + 31o = 180o 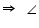 BAC = 180o - 100º
BAC = 180o - 100º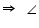 BAC = 80o
BAC = 80o 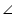 BDC =
BDC = 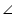 BAC = 80o (Angles in same segment of circle are equal)
BAC = 80o (Angles in same segment of circle are equal)
Question 5
In the given figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that  BEC = 130o and
BEC = 130o and  ECD = 20o. Find
ECD = 20o. Find  BAC.
BAC. 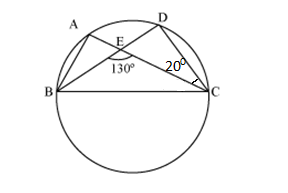
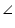 BEC = 130o and
BEC = 130o and 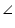 ECD = 20o. Find
ECD = 20o. Find 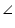 BAC.
BAC. 
Solution 5
In 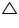 CDE
CDE
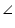 CDE +
CDE + 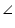 DCE =
DCE = 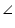 CEB (Exterior angle)
CEB (Exterior angle)
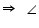 CDE + 20o = 130o
CDE + 20o = 130o 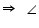 CDE = 110o
CDE = 110o
But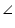 BAC =
BAC = 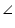 CDE (Angles in same segment of circle)
CDE (Angles in same segment of circle)
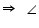 BAC = 110o
BAC = 110o
 CDE
CDE CDE +
CDE +  DCE =
DCE =  CEB (Exterior angle)
CEB (Exterior angle)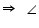 CDE + 20o = 130o
CDE + 20o = 130o 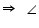 CDE = 110o
CDE = 110oBut
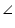 BAC =
BAC = 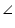 CDE (Angles in same segment of circle)
CDE (Angles in same segment of circle) BAC = 110o
BAC = 110o
Question 6
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If  DBC = 70o,
DBC = 70o,  BAC is 30o, find
BAC is 30o, find  BCD. Further, if AB = BC, find
BCD. Further, if AB = BC, find  ECD.
ECD.
 DBC = 70o,
DBC = 70o,  BAC is 30o, find
BAC is 30o, find  BCD. Further, if AB = BC, find
BCD. Further, if AB = BC, find  ECD.
ECD.
Solution 6
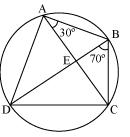 For chord CD
For chord CD  CBD =
CBD =  CAD (Angles in same segment)
CAD (Angles in same segment)  CAD = 70o
CAD = 70o  BAD =
BAD =  BAC +
BAC +  CAD = 30o + 70o = 100o
CAD = 30o + 70o = 100o  BCD +
BCD +  BAD = 180o (Opposite angles of a cyclic quadrilateral)
BAD = 180o (Opposite angles of a cyclic quadrilateral) BCD + 100o = 180o
BCD + 100o = 180o BCD = 80o
BCD = 80o In
 ABC AB = BC (given)
ABC AB = BC (given) BCA =
BCA =  CAB (Angles opposite to equal sides of a triangle)
CAB (Angles opposite to equal sides of a triangle)  BCA = 30o
BCA = 30oWe have
 BCD = 80o
BCD = 80o BCA +
BCA +  ACD = 80o
ACD = 80o 30o +
 ACD = 80o
ACD = 80o  ACD = 50o
ACD = 50o  ECD = 50o
ECD = 50o
Question 7
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Solution 7
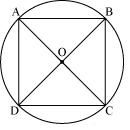 Let ABCD a cyclic quadrilateral having diagonals as BD and AC intersecting each other at point O.
Let ABCD a cyclic quadrilateral having diagonals as BD and AC intersecting each other at point O. 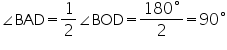 (Consider BD as a chord)
(Consider BD as a chord)  BCD +
BCD +  BAD = 180o (Cyclic quadrilateral)
BAD = 180o (Cyclic quadrilateral)  BCD = 180o - 90o = 90o
BCD = 180o - 90o = 90o 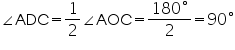 (Considering AC as a chord)
(Considering AC as a chord)  ADC +
ADC +  ABC = 180o (Cyclic quadrilateral)
ABC = 180o (Cyclic quadrilateral) 90o +
 ABC = 180o
ABC = 180o ABC = 90o
ABC = 90oHere, each interior angle of cyclic quadrilateral is of 90o. Hence it is a rectangle.
Question 8
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Solution 8
 Consider a trapezium ABCD with AB | |CD and BC = AD Draw AM
Consider a trapezium ABCD with AB | |CD and BC = AD Draw AM  CD and BN
CD and BN  CD
CDIn
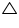 AMD and
AMD and 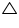 BNC
BNCAD = BC (Given)
 AMD =
AMD =  BNC (By construction each is 90o)
BNC (By construction each is 90o)AM = BM (Perpendicular distance between two parallel lines is same)
 AMD
AMD  BNC (RHS congruence rule)
BNC (RHS congruence rule)  ADC =
ADC =  BCD (CPCT) ... (1)
BCD (CPCT) ... (1)  BAD and
BAD and  ADC are on same side of transversal AD
ADC are on same side of transversal AD  BAD +
BAD +  ADC = 180o ... (2)
ADC = 180o ... (2)  BAD +
BAD +  BCD = 180o [Using equation (1)]
BCD = 180o [Using equation (1)] This equation shows that the opposite angles are supplementary.
So, ABCD is a cyclic quadrilateral.
Question 9
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that  ACP =
ACP =  QCD
QCD 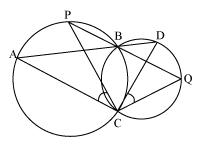
 ACP =
ACP =  QCD
QCD 
Solution 9
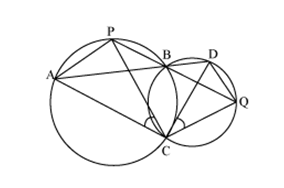 Join chords AP and DQ
Join chords AP and DQ For chord AP
 PBA =
PBA = 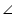 ACP (Angles in same segment) ... (1)
ACP (Angles in same segment) ... (1) For chord DQ
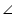 DBQ =
DBQ = 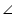 QCD (Angles in same segment) ... (2)
QCD (Angles in same segment) ... (2) ABD and PBQ are line segments intersecting at B.
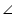 PBA =
PBA = 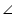 DBQ (Vertically opposite angles) ... (3)
DBQ (Vertically opposite angles) ... (3) From equations (1), (2) and (3), we have
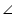 ACP =
ACP = 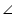 QCD
QCD
Question 10
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Solution 10
 Consider a
Consider a 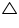 ABC
ABCTwo circles are drawn while taking AB and AC as diameter.
Let they intersect each other at D and let D does not lie on BC.
Join AD
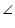 ADB = 90o (Angle subtend by semicircle)
ADB = 90o (Angle subtend by semicircle)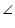 ADC = 90o (Angle subtend by semicircle)
ADC = 90o (Angle subtend by semicircle)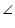 BDC =
BDC = 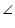 ADB +
ADB +  ADC = 90o + 90o = 180o
ADC = 90o + 90o = 180o Hence BDC is straight line and our assumption was wrong.
Thus, Point D lies on third side BC of
 ABC
ABC 
Question 11
ABC and ADC are two right triangle with common hypotenuse AC. Prove that  CAD =
CAD =  CBD.
CBD.
 CAD =
CAD =  CBD.
CBD.
Solution 11
 In
In 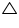 ABC
ABC  ABC +
ABC +  BCA +
BCA +  CAB = 180o (Angle sum property of a triangle)
CAB = 180o (Angle sum property of a triangle)  90o +
90o +  BCA +
BCA +  CAB = 180o
CAB = 180o
 BCA +
BCA +  CAB = 90o ... (1)
CAB = 90o ... (1) In
 ADC
ADC  CDA +
CDA +  ACD +
ACD +  DAC = 180o (Angle sum property of a triangle)
DAC = 180o (Angle sum property of a triangle) 90o +
90o +  ACD +
ACD +  DAC = 180o
DAC = 180o
 ACD +
ACD +  DAC = 90o ... (2)
DAC = 90o ... (2) Adding equations (1) and (2), we have
 BCA +
BCA +  CAB +
CAB +  ACD +
ACD +  DAC = 180o
DAC = 180o  (
( BCA +
BCA +  ACD) + (
ACD) + ( CAB +
CAB +  DAC) = 180o
DAC) = 180o  BCD +
BCD +  DAB = 180o ... (3)
DAB = 180o ... (3) But it is given that
 B +
B +  D = 90o + 90o = 180o ... (4)
D = 90o + 90o = 180o ... (4) From equations (3) and (4), we can see that quadrilateral ABCD is having sum of measures of opposite angles as 180o.
So, it is a cyclic quadrilateral.
Consider chord CD.
Now,
 CAD =
CAD =  CBD (Angles in same segment)
CBD (Angles in same segment) 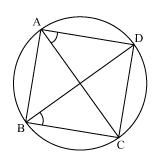
Question 12
Prove that a cyclic parallelogram is a rectangle.
Solution 12
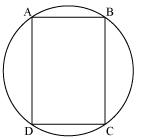 Let ABCD be a cyclic parallelogram.
Let ABCD be a cyclic parallelogram.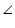 A +
A + 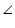 C = 180o (Opposite angle of cyclic quadrilateral) ... (1)
C = 180o (Opposite angle of cyclic quadrilateral) ... (1)We know that opposite angles of a parallelogram are equal
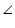 A =
A = 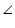 C and
C and 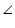 B =
B = 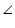 D
D From equation (1)
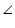 A +
A + 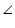 C = 180o
C = 180o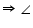 A +
A + 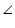 A = 180o
A = 180o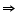 2
2 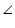 A = 180o
A = 180o A = 90o
A = 90o Parallelogram ABCD is having its one of interior angles as 90o, so, it is a rectangle.
NCERT Solution for Class 9 Mathematics Chapter 10 - Circles Page/Excercise 10.6
Question 1
Prove that line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Solution 1
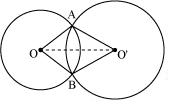
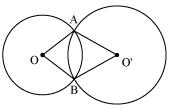 Let two circles having their centres as O and intersect each other at point A and B respectively.
Let two circles having their centres as O and intersect each other at point A and B respectively. Construction: Let us join OO',
 Now in
Now in  AOO' and
AOO' and 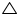 BOO'
BOO' OA = OB (radius of circle 1)
O'A = O'B (radius of circle 2)
OO' = OO' (common)
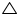 AOO'
AOO' 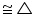 BOO' (by SSS congruence rule)
BOO' (by SSS congruence rule) 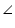 OAO' =
OAO' =  OBO' (by CPCT)
OBO' (by CPCT) So, line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Question 2
Two chords AB and CD of lengths 5 cm and 11cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Solution 2
Draw OM  AB and ON
AB and ON  CD. Join OB and OD
CD. Join OB and OD 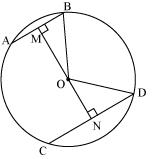
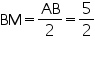 (Perpendicular from centre bisects the chord)
(Perpendicular from centre bisects the chord) 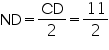 Let ON be x, so OM will be 6 - x
Let ON be x, so OM will be 6 - x
In MOB
MOB 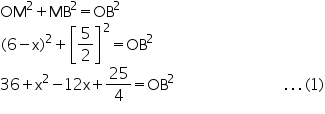 In
In  NOD
NOD 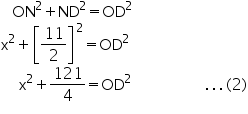 We have OB = OD (radii of same circle)
We have OB = OD (radii of same circle)
So, from equation (1) and (2)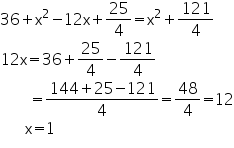 From equation (2)
From equation (2)  So, radius of circle is found to be
So, radius of circle is found to be 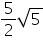 cm.
cm.
 AB and ON
AB and ON  CD. Join OB and OD
CD. Join OB and OD 
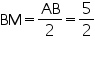 (Perpendicular from centre bisects the chord)
(Perpendicular from centre bisects the chord) 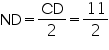 Let ON be x, so OM will be 6 - x
Let ON be x, so OM will be 6 - x In
 MOB
MOB 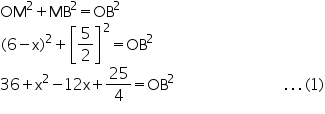 In
In  NOD
NOD 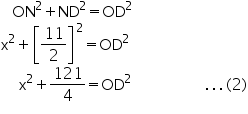 We have OB = OD (radii of same circle)
We have OB = OD (radii of same circle)So, from equation (1) and (2)
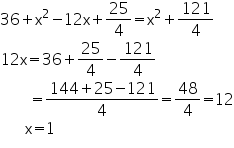 From equation (2)
From equation (2)  So, radius of circle is found to be
So, radius of circle is found to be 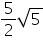 cm.
cm.
Question 3
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord form the centre?
Solution 3
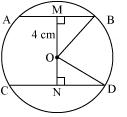 Distance of smaller chord AB from centre of circle = 4 cm.
Distance of smaller chord AB from centre of circle = 4 cm.OM = 4 cm
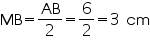 In
In  OMB
OMB 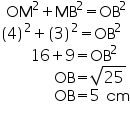 In
In  OND OD=OB=5cm (radii of same circle)
OND OD=OB=5cm (radii of same circle) 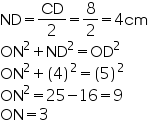 So, distance of bigger chord from centre is 3 cm.
So, distance of bigger chord from centre is 3 cm.
Question 4
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that  ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
 ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Solution 4
 In
In  AOD and
AOD and  COE
COEOA = OC (radii of same circle)
OD = OE (radii of same circle)
AD = CE (given)
 AOD
AOD  COE (SSS congruence rule)
COE (SSS congruence rule)  OAD =
OAD =  OCE (by CPCT) ... (1)
OCE (by CPCT) ... (1)  ODA =
ODA =  OEC (by CPCT) ... (2)
OEC (by CPCT) ... (2)We also have
 OAD =
OAD =  ODA (As OA = OD) ... (3)
ODA (As OA = OD) ... (3)From equations (1), (2) and (3), we have
 OAD =
OAD =  OCE =
OCE =  ODA =
ODA =  OEC
OEC Let
 OAD =
OAD =  OCE =
OCE =  ODA =
ODA =  OEC = x
OEC = xIn
 OAC,
OAC,OA = OC
 OCA =
OCA =  OAC (let a) In
OAC (let a) In  ODE,
ODE,OD = OE
 OED =
OED =  ODE (let y)
ODE (let y)ADEC is a cyclic quadrilateral
 CAD +
CAD +  DEC = 180o (opposite angles are supplementary) x + a + x + y = 180o
DEC = 180o (opposite angles are supplementary) x + a + x + y = 180o2x + a + y = 180o
y = 180� - 2x - a ... (4)
But
 DOE = 180� - 2y
DOE = 180� - 2yAnd
 AOC = 180� - 2a
AOC = 180� - 2aNow,
 DOE -
DOE -  AOC = 2a - 2y = 2a - 2 (180� - 2x - a)
AOC = 2a - 2y = 2a - 2 (180� - 2x - a)= 4a + 4x - 360o ... (5)
Now,
 BAC +
BAC +  CAD = 180� (Linear pair)
CAD = 180� (Linear pair)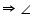 BAC = 180� -
BAC = 180� -  CAD = 180� - (a + x)
CAD = 180� - (a + x)Similarly,
 ACB = 180� - (a + x)
ACB = 180� - (a + x) Now, in
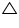 ABC
ABC ABC +
ABC +  BAC +
BAC +  ACB = 180� (Angle sum property of a triangle)
ACB = 180� (Angle sum property of a triangle) ABC = 180� -
ABC = 180� -  BAC -
BAC -  ACB
ACB= 180� - (180� - a - x) - (180� - a -x)
= 2a + 2x - 180�
=
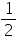 [4a + 4x - 360o]
[4a + 4x - 360o] ABC =
ABC = 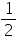 [
[ DOE -
DOE -  AOC] [Using equation (5)]
AOC] [Using equation (5)]
Question 5
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
Solution 5
 Let ABCD be a rhombus in which diagonals are intersecting at point O and a circle is drawn taking side CD as its diameter.
Let ABCD be a rhombus in which diagonals are intersecting at point O and a circle is drawn taking side CD as its diameter. We know that angle in a semicircle is of 90o.
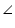 COD = 90o
COD = 90o Also in rhombus the diagonals intersect each other at 90o
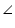 AOB =
AOB = 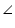 BOC =
BOC = 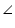 COD =
COD =  DOA = 90o
DOA = 90o So, point O has to lie on the circle.
Question 6
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E prove that AE = AD
Solution 6
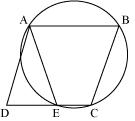 We see that ABCE is a cyclic quadrilateral and in a cyclic quadrilateral sum of opposite angles is 180o
We see that ABCE is a cyclic quadrilateral and in a cyclic quadrilateral sum of opposite angles is 180o AEC +
AEC +  CBA = 180o
CBA = 180o  AEC +
AEC +  AED = 180o (linear pair)
AED = 180o (linear pair) AED =
AED =  CBA ... (1)
CBA ... (1) For a parallelogram opposite angles are equal.
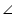 ADE =
ADE = 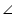 CBA ... (2)
CBA ... (2)From (1) and (2)
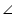 AED =
AED = 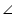 ADE
ADEAD = AE (angles opposite to equal sides of a triangle)
Question 7
AC and BD are chords of a circle which bisect each other. Prove that
(i) AC and BD are diameters,
(ii) ABCD is a rectangle.
(i) AC and BD are diameters,
(ii) ABCD is a rectangle.
Solution 7
 Let two chords AB and CD are intersecting each other at point O.
Let two chords AB and CD are intersecting each other at point O.In
 AOB and
AOB and  COD
CODOA = OC (given)
OB = OD (given)
 AOB =
AOB =  COD (vertically opposite angles)
COD (vertically opposite angles) AOB
AOB  COD (SAS congruence rule)
COD (SAS congruence rule) AB = CD (by CPCT)
Similarly, we can prove
 AOD
AOD  COB
COBHence, ACBD is a parallelogram.
We know that opposite angles of a parallelogram are equal
 A =
A = 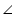 C But
C But 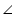 A +
A + 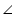 C = 180o (ABCD is a cyclic quadrilateral)
C = 180o (ABCD is a cyclic quadrilateral)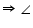 A +
A + 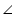 A = 180o
A = 180o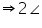 A = 180o
A = 180o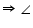 A = 90o
A = 90oAs ACBD is a parallelogram and one of its interior angles is 90o, so it is a rectangle.
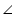 A is the angle subtended by chord BD. And as
A is the angle subtended by chord BD. And as  A = 90o, so BD should be diameter of circle. Similarly AC is diameter of circle.
A = 90o, so BD should be diameter of circle. Similarly AC is diameter of circle.
Question 8
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90o 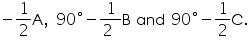
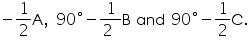
Solution 8
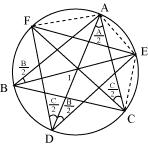
It is given that BE is the bisector of
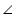 B
B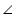 ABE =
ABE = 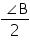
But
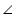 ADE =
ADE = 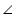 ABE (angles in same segment for chord AE)
ABE (angles in same segment for chord AE)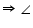 ADE =
ADE = 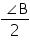
Similarly,
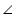 ACF =
ACF = 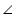 ADF =
ADF = 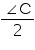 (angle in same segment for chord AF)
(angle in same segment for chord AF) Now,
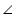 D =
D = 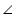 ADE +
ADE + 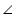 ADF
ADF  Similarly we can prove that
Similarly we can prove that 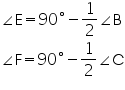
Question 9
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Solution 9
 AB is common chord in both congruent circles.
AB is common chord in both congruent circles.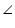 APB =
APB = 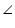 AQB
AQB Now in
 BPQ
BPQ  APB =
APB =  AQB
AQB
Question 10
In any triangle ABC, if the angle bisector of  A and perpendicular bisector of BC intersect, prove that they intersect on the circum circle of the triangle ABC.
A and perpendicular bisector of BC intersect, prove that they intersect on the circum circle of the triangle ABC.
 A and perpendicular bisector of BC intersect, prove that they intersect on the circum circle of the triangle ABC.
A and perpendicular bisector of BC intersect, prove that they intersect on the circum circle of the triangle ABC.
Solution 10
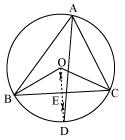 Let perpendicular bisector of side BC and angle bisector of
Let perpendicular bisector of side BC and angle bisector of  A meet at point D.
A meet at point D.Let perpendicular bisector of side BC intersects it at E.
Perpendicular bisector of side BC will pass through circum centre O of circle. Now,
 BOC and
BOC and  BAC are the angles subtended by arc BC at the centre and a point A on the remaining part of the circle respectively.
BAC are the angles subtended by arc BC at the centre and a point A on the remaining part of the circle respectively. We also know that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
 BOC = 2
BOC = 2  BAC = 2
BAC = 2 A ... (1)
A ... (1) In
 BOE and
BOE and  COE OE = OE (common)
COE OE = OE (common)OB = OC (radii of same circle)
 OEB =
OEB =  OEC (Each 90o as OD
OEC (Each 90o as OD  BC)
BC)  BOE
BOE  COE (RHS congruence rule)
COE (RHS congruence rule)  BOE =
BOE =  COE (by CPCT) ... (2)
COE (by CPCT) ... (2) But
 BOE +
BOE +  COE =
COE =  BOC
BOC  BOE +
BOE + BOE = 2
BOE = 2 A [Using equations (1) and (2)]
A [Using equations (1) and (2)]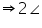 BOE = 2
BOE = 2 A
A  BOE =
BOE =  A
A  BOE =
BOE =  COE =
COE =  A The perpendicular bisector of side BC and angle bisector of
A The perpendicular bisector of side BC and angle bisector of  A meet at point D.
A meet at point D.  BOD =
BOD =  BOE =
BOE =  A ... (3) Since AD is the bisector of angle
A ... (3) Since AD is the bisector of angle  A
A  BAD =
BAD = 
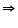 2
2 BAD =
BAD =  A ... (4)
A ... (4)From equations (3) and (4), we have
 BOD = 2
BOD = 2 BAD
BAD It is possible only if BD will be a chord of the circle. For this the point D lies on circum circle.
Therefore, the perpendicular bisector of side BC and angle bisector of
 A meet on the circum circle of triangle ABC.
A meet on the circum circle of triangle ABC.
No comments:
Post a Comment