NCERT Solution for Class 10 Mathematics Chapter 8 - Trigonometry Page/Excercise 8.1
Question 1
In  ABC right angled at B, AB = 24 cm, BC = 7 m. Determine
ABC right angled at B, AB = 24 cm, BC = 7 m. Determine
(i) sin A, cos A
(ii) sin C, cos C
 ABC right angled at B, AB = 24 cm, BC = 7 m. Determine
ABC right angled at B, AB = 24 cm, BC = 7 m. Determine(i) sin A, cos A
(ii) sin C, cos C
Solution 1
In  ABC by applying Pythagoras theorem
ABC by applying Pythagoras theorem
AC2 = AB2 + BC2
= (24)2 + (7)2
= 576 + 49
= 625
AC =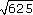 = 25 cm
= 25 cm



 ABC by applying Pythagoras theorem
ABC by applying Pythagoras theorem AC2 = AB2 + BC2
= (24)2 + (7)2
= 576 + 49
= 625
AC =



Question 2
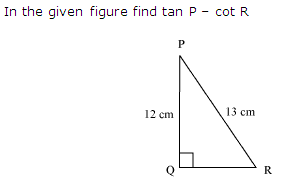
Solution 2
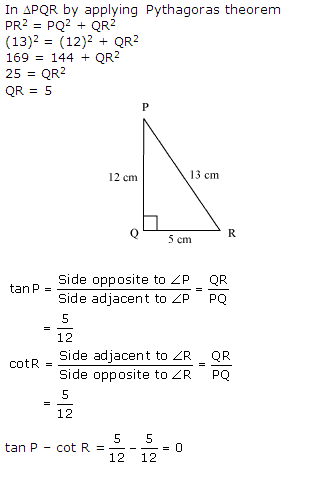
Question 3
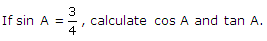
Solution 3

Question 4
Given 15 cot A = 8. Find sin A and sec A
Solution 4
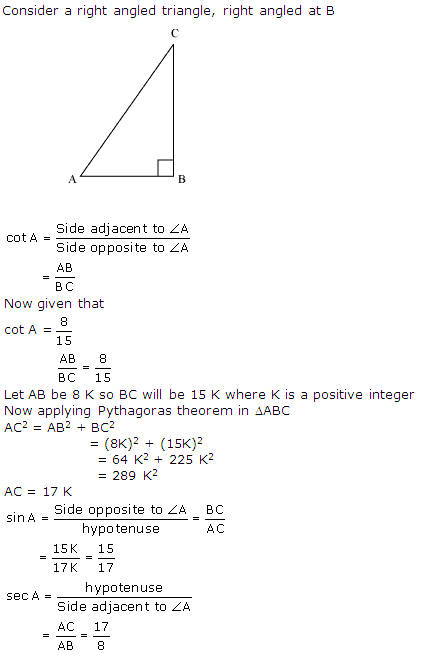
Question 5

Solution 5

Question 6

Solution 6
Question 7
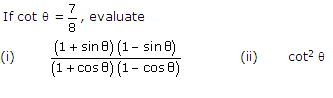
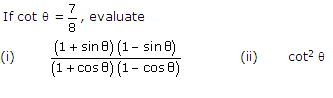
Solution 7
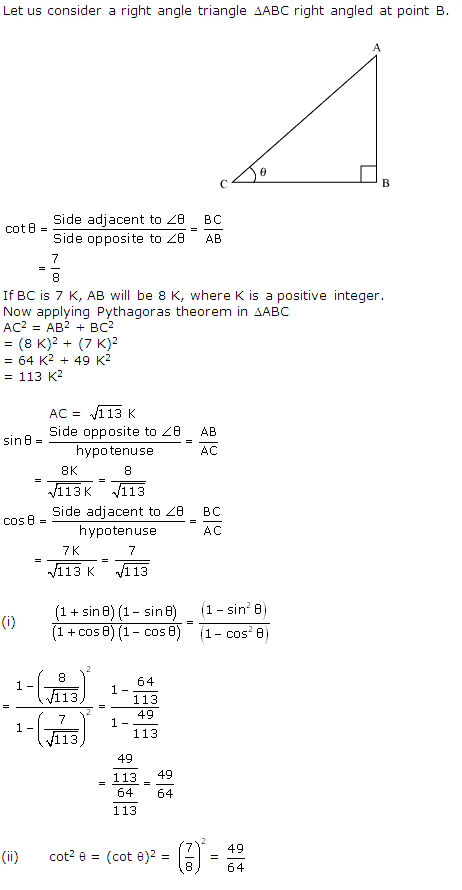
Question 8
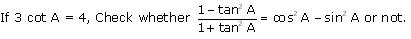
Solution 8

Question 9


Solution 9
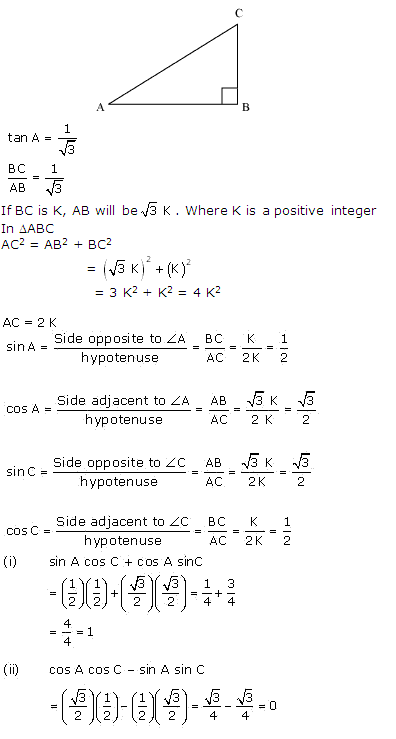
Question 10

Solution 10
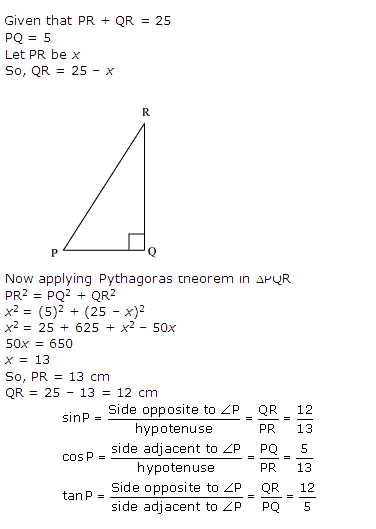
Question 11


Solution 11

NCERT Solution for Class 10 Mathematics Chapter 8 - Trigonometry Page/Excercise 8.2
Question 1
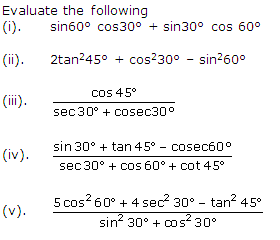
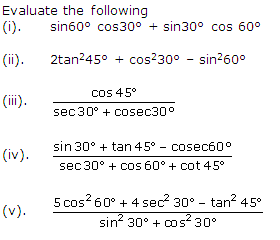
Solution 1
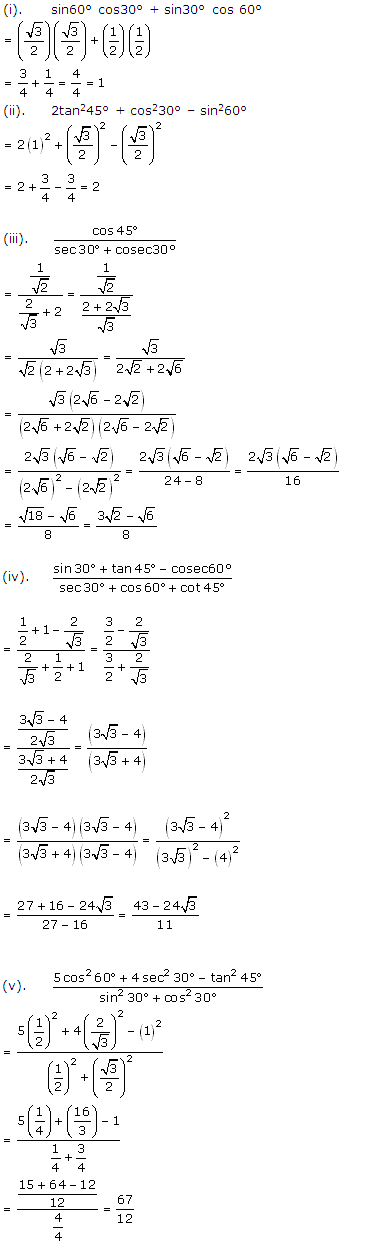
Question 2
Choose the correct option and justify your choice.
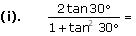
(A). sin60°
(B). cos60°
(C). tan60°
(D). sin30°
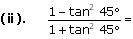
(A). tan90°
(B). 1
(C). sin45°
(D). 0
(iii). sin2A = 2sinA is true when A =
(A). 0°
(B). 30°
(C). 45°
(D). 60°
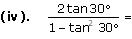
(A). cos60°
(B). sin60°
(C). tan60°
(D). sin30°
(A). sin60°
(B). cos60°
(C). tan60°
(D). sin30°
(A). tan90°
(B). 1
(C). sin45°
(D). 0
(iii). sin2A = 2sinA is true when A =
(A). 0°
(B). 30°
(C). 45°
(D). 60°
(A). cos60°
(B). sin60°
(C). tan60°
(D). sin30°
Solution 2

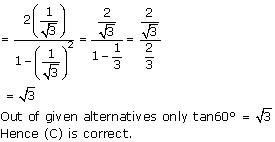
Question 3
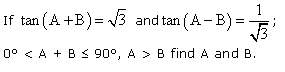
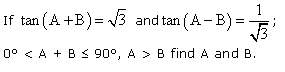
Solution 3
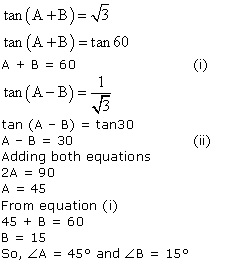
Question 4
State whether the following are true or false. Justify your answer.
(i). sin(A + B) = sinA + sinB
(ii). The value of sinθ increases as θ increases
(iii). The value of cosθ increases as θ increases
(iv). sinθ = cosθ for all values of θ
(v). cotA is not defined for A = 0�
(i). sin(A + B) = sinA + sinB
(ii). The value of sinθ increases as θ increases
(iii). The value of cosθ increases as θ increases
(iv). sinθ = cosθ for all values of θ
(v). cotA is not defined for A = 0�
Solution 4

NCERT Solution for Class 10 Mathematics Chapter 8 - Trigonometry Page/Excercise 8.3
Question 1
Evaluate
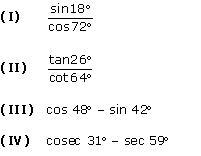
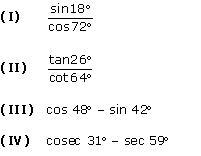
Solution 1
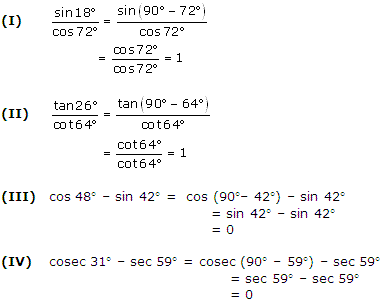
Question 2
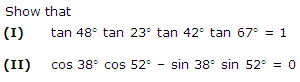
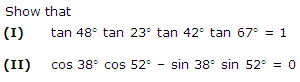
Solution 2
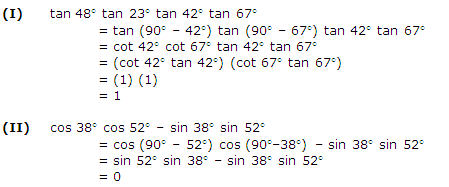
Question 3
If tan 2A = cot (A - 18�), where 2A is an acute angle, find the value of A.
Solution 3
Given that
tan 2A = cot (A - 18�)
cot (90� - 2A) = cot (A -18�)
90� - 2A = A - 18�
108� = 3A
A = 36�
tan 2A = cot (A - 18�)
cot (90� - 2A) = cot (A -18�)
90� - 2A = A - 18�
108� = 3A
A = 36�
Question 4
If tan A = cot B, prove that A + B = 90�
Solution 4
Given that
tan A = cot B
tan A = tan (90� - B)
A = 90� - B
A + B = 90�
tan A = cot B
tan A = tan (90� - B)
A = 90� - B
A + B = 90�
Question 5
If sec 4A = cosec (A - 20�), where 4A is an acute angle, find the value of A.
Solution 5
Given that
Sec 4A = cosec (A - 20�)
Cosec (90� - 4A) = cosec (A - 20�)
90� - 4A = A - 20�
110� = 5A
A = 22�
Sec 4A = cosec (A - 20�)
Cosec (90� - 4A) = cosec (A - 20�)
90� - 4A = A - 20�
110� = 5A
A = 22�
Question 6
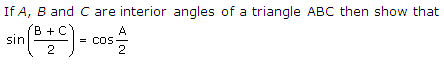
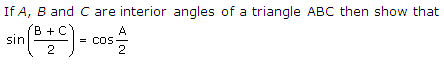
Solution 6
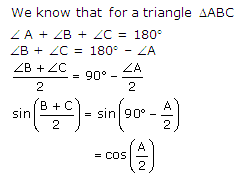
Question 7
Express sin 67� + cos 75� in terms of trigonometric ratios of angles between 0� and 45�.
Solution 7
sin 67� + cos 75�
= sin (90� - 23�) + cos (90� - 15�)
= cos 23� + sin 15�
= sin (90� - 23�) + cos (90� - 15�)
= cos 23� + sin 15�
NCERT Solution for Class 10 Mathematics Chapter 8 - Trigonometry Page/Excercise 8.4
Question 1
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Solution 1
We know that


Question 2
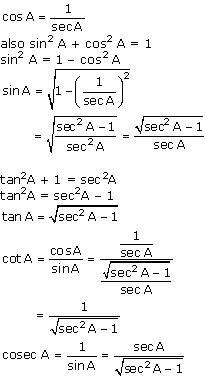
Write all the other trigonometric ratios of  A in terms of sec A.
A in terms of sec A.
 A in terms of sec A.
A in terms of sec A.
Solution 2
We know that

Question 3
Evaluate
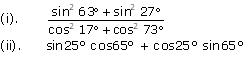
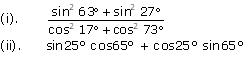
Solution 3
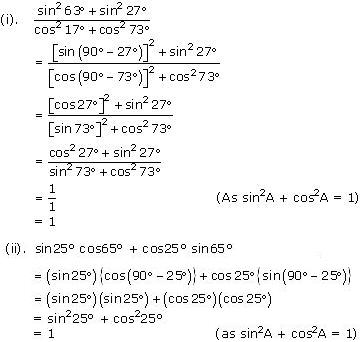
Question 4
Choose the correct option. Justify your choice.
(i). 9sec2 A - 9tan2 A =
(A) 1
(B) 9
(C) 8
(D) 0
(ii). (1 + tanθ + secθ) (1 + cotθ - cosecθ)
(A) 0
(B) 1
(C) 2
(D) -1
(iii). (secA + tanA) (1 - sinA) =
(A) secA
(B) sinA
(C) cosecA
(D) cosA
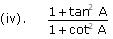
(A) sec2A
(B) -1
(C) cot2A
(D) tan2A
(i). 9sec2 A - 9tan2 A =
(A) 1
(B) 9
(C) 8
(D) 0
(ii). (1 + tanθ + secθ) (1 + cotθ - cosecθ)
(A) 0
(B) 1
(C) 2
(D) -1
(iii). (secA + tanA) (1 - sinA) =
(A) secA
(B) sinA
(C) cosecA
(D) cosA
(A) sec2A
(B) -1
(C) cot2A
(D) tan2A
Solution 4
(i) 9sec2A - 9tan2A
= 9(sec2A - tan2A)
= 9 (1) [as sec2 A - tan2 A = 1]
= 9
Hence alternative (B) is correct.
(ii) (1 + tanθ + secθ) (1 + cotθ - cosecθ)
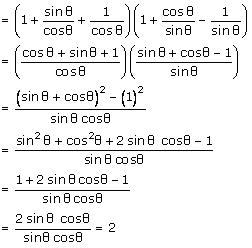
Hence alternative (C) is correct.
(iii) (secA + tanA) (1 - sinA)
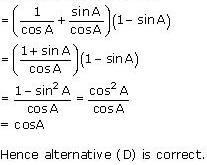
(iv)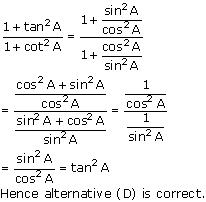
= 9(sec2A - tan2A)
= 9 (1) [as sec2 A - tan2 A = 1]
= 9
Hence alternative (B) is correct.
(ii) (1 + tanθ + secθ) (1 + cotθ - cosecθ)
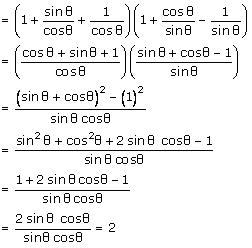
Hence alternative (C) is correct.
(iii) (secA + tanA) (1 - sinA)
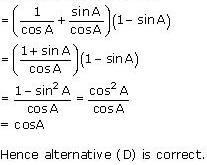
(iv)
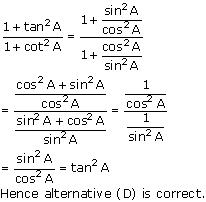
Question 5
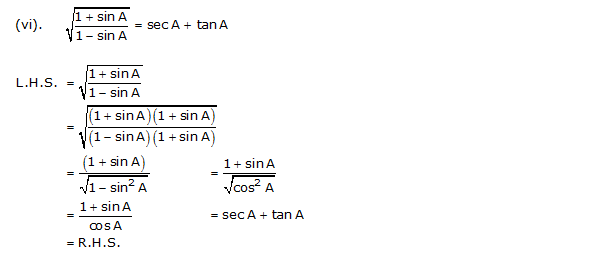
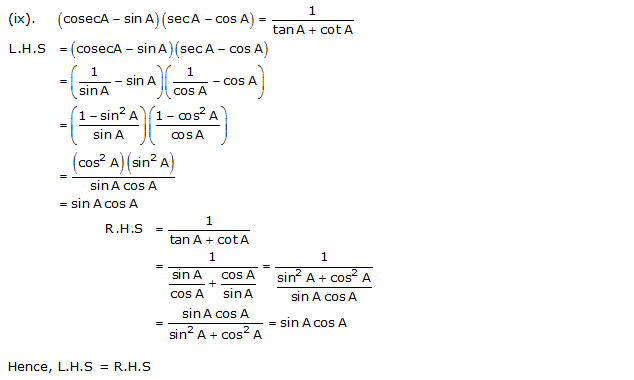
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
Solution 5
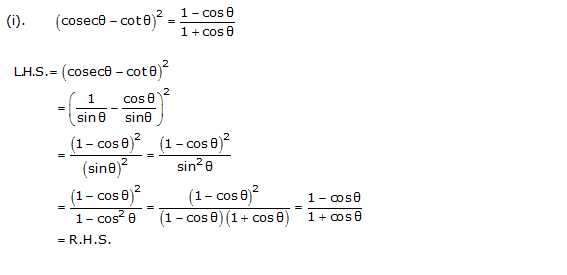





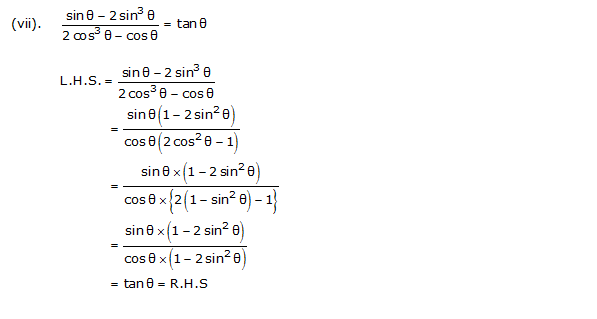

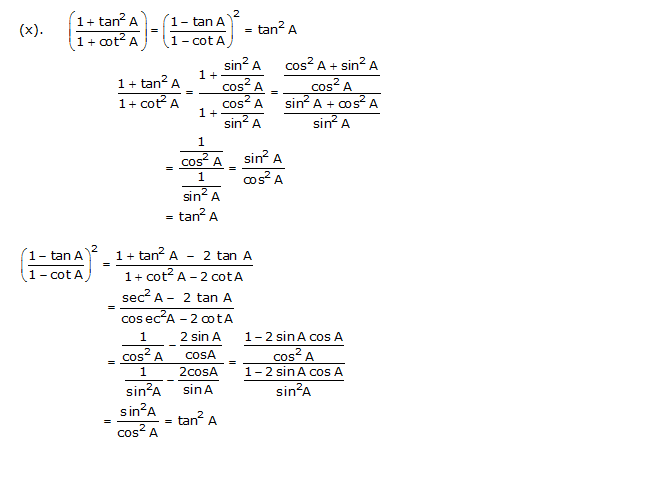
No comments:
Post a Comment