NCERT Solution for Class 10 Mathematics Chapter 10 - Circles RR ACADEMY MEERUT

NCERT Solution for Class 10 Mathematics Chapter 10 - Circles Page/Excercise 10.1

Question 1

Solution 1

Question 2

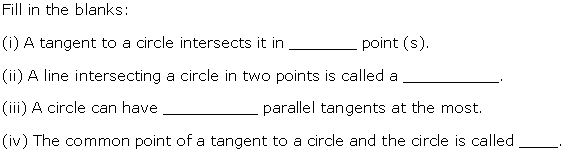
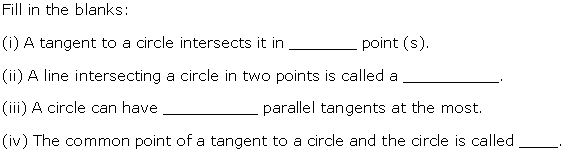
Solution 2

Question 3

Solution 3

Question 4

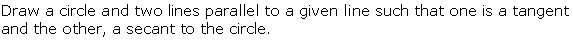
Solution 4

NCERT Solution for Class 10 Mathematics Chapter 10 - Circles Page/Excercise 10.2

Question 1

Solution 1

Question 2

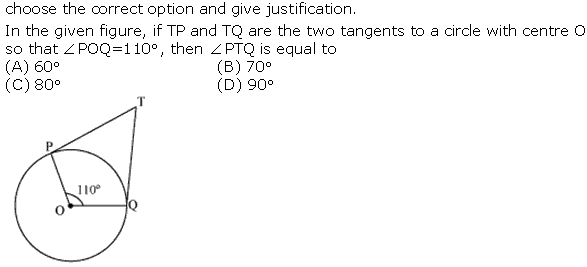
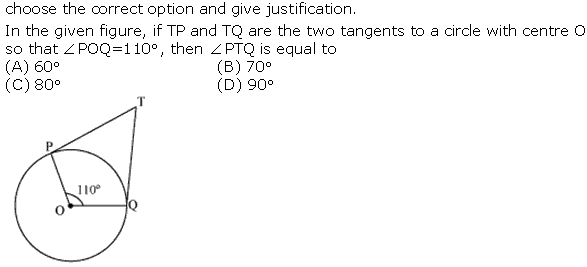
Solution 2

Question 3

Solution 3

  

Question 4

Solution 4

Question 5

Solution 5

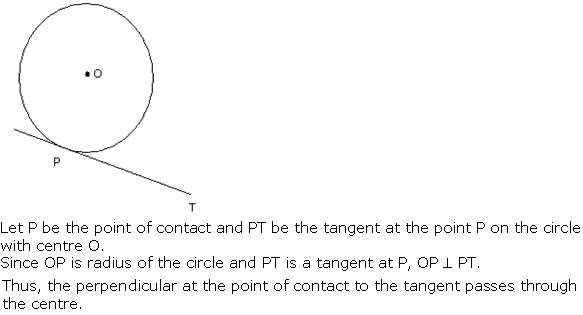
Question 6

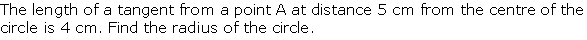
Solution 6

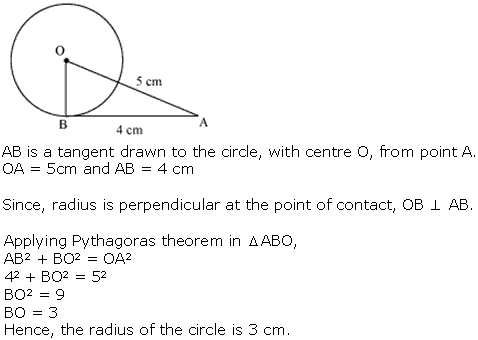
Question 7

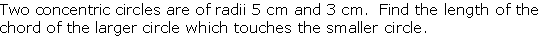
Solution 7

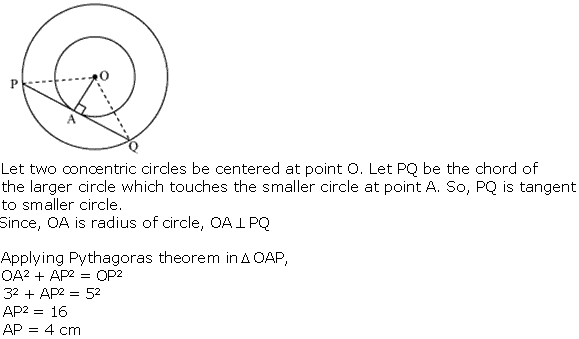
Question 8

Solution 8

Question 9

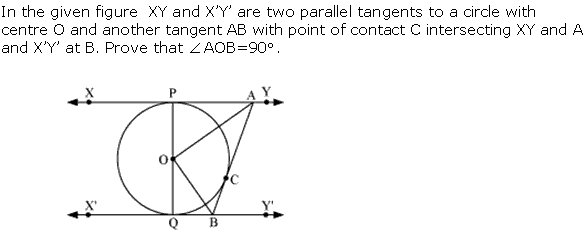
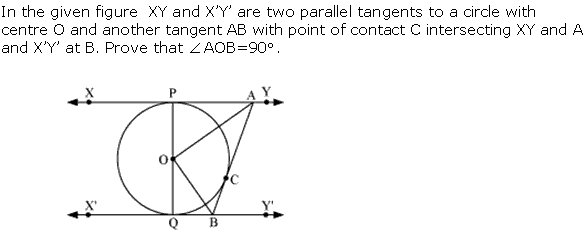
Solution 9

Question 10

Solution 10

Question 11

Prove that the parallelogram circumscribing a circle is a rhombus.

Solution 11

Since, ABCD is a parallelogram,

AB = CD                                                                (i)

BC = AD                                                                (ii)

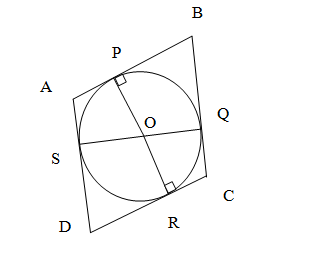
Now, it can be observed that:

DR = DS                 (tangents on circle from point D)

CR = CQ                 (tangents on circle from point C)

BP = BQ                 (tangents on circle from point B)

AP = AS                 (tangents on circle from point A)

Adding all the above four equations,

DR + CR + BP + AP = DS + CQ + BQ + AS

(DR + CR) + (BP + AP) = (DS + AS) + (CQ + BQ)                 

CD + AB = AD + BC                                            (iii)

From equation (i) (ii)  and (ii):

         2AB = 2BC

         AB = BC

         AB = BC = CD = DA

         Hence, ABCD is a rhombus.

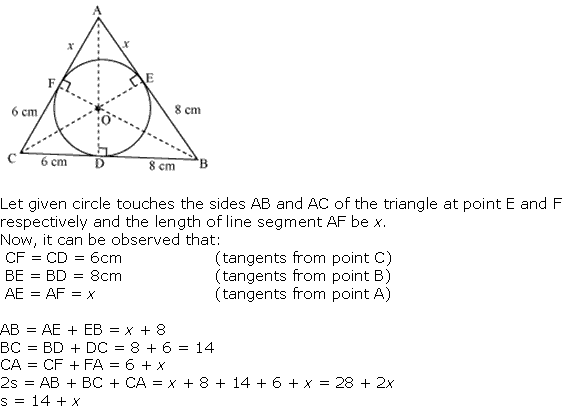
Question 12

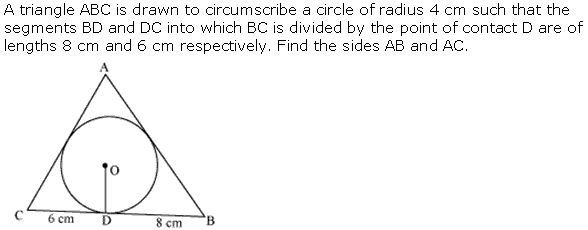
Solution 12

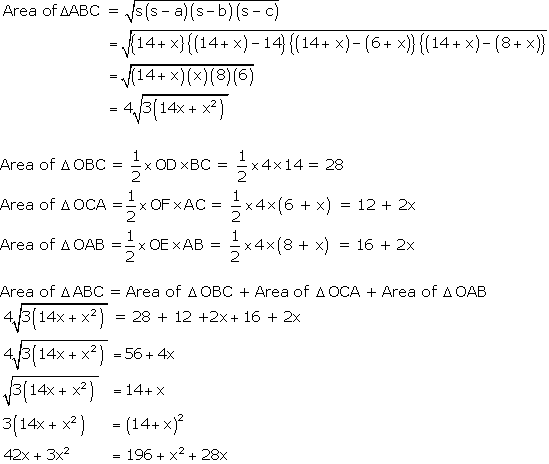
Question 13

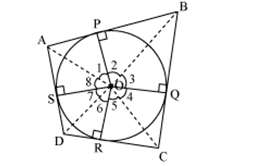
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

Solution 13