NCERT Solution for Class 9 Mathematics Chapter 7 - Triangles Page/Excercise 7.1
Question 1
In quadrilateral ACBD, AC = AD and AB bisects 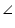 A (See the given figure). Show that
A (See the given figure). Show that 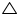 ABC
ABC 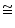
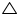 ABD. What can you say about BC and BD?
ABD. What can you say about BC and BD? 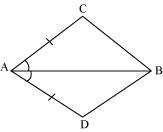
 A (See the given figure). Show that
A (See the given figure). Show that  ABC
ABC 
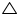 ABD. What can you say about BC and BD?
ABD. What can you say about BC and BD? 
Solution 1
In 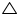 ABC and
ABC and 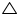 ABD
ABD
AC = AD (given)
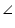 CAB =
CAB = 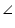 DAB (given)
DAB (given)
AB = AB (common) So, BC and BD are of equal length.
So, BC and BD are of equal length.
 ABC and
ABC and  ABD
ABDAC = AD (given)
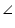 CAB =
CAB = 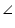 DAB (given)
DAB (given)AB = AB (common)
Question 2
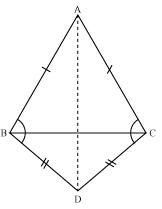
ABCD is a quadrilateral in which AD = BC and 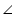 DAB =
DAB = 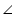 CBA (See the given figure). Prove that
CBA (See the given figure). Prove that
(i) 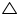 ABD
ABD 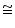
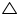 BAC
BAC
(ii) BD = AC
(iii) 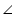 ABD =
ABD =  BAC.
BAC. 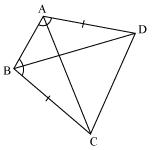
 DAB =
DAB =  CBA (See the given figure). Prove that
CBA (See the given figure). Prove that (i)
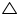 ABD
ABD 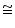
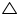 BAC
BAC(ii) BD = AC
(iii)
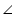 ABD =
ABD = 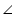 BAC.
BAC. 
Solution 2
In 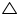 ABD and
ABD and 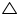 BAC
BAC
AD = BC (given)
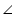 DAB =
DAB = 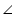 CBA (given)
CBA (given)
AB = BA (common)
And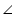 ABD =
ABD = 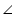 BAC (by CPCT)
BAC (by CPCT)
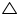 ABD and
ABD and 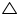 BAC
BACAD = BC (given)
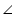 DAB =
DAB = 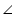 CBA (given)
CBA (given)AB = BA (common)
And
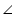 ABD =
ABD = 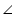 BAC (by CPCT)
BAC (by CPCT)
Question 3
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB. 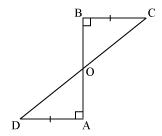

Solution 3
In  BOC and
BOC and  AOD
AOD
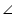 BOC =
BOC = 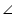 AOD (vertically opposite angles)
AOD (vertically opposite angles)
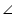 CBO =
CBO = 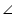 DAO (each 90o)
DAO (each 90o)
BC = AD (given)
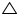 BOC and
BOC and 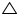 AOD
AOD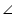 BOC =
BOC = 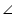 AOD (vertically opposite angles)
AOD (vertically opposite angles)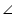 CBO =
CBO = 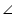 DAO (each 90o)
DAO (each 90o)BC = AD (given)

Question 4
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that 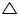 ABC
ABC 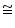
 CDA.
CDA. 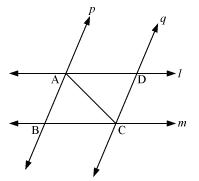
 ABC
ABC 
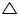 CDA.
CDA. 
Solution 4

Question 5
Line l is the bisector of an angle 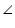 A and B is any point on l. BP and BQ are perpendiculars from B to the arms of
A and B is any point on l. BP and BQ are perpendiculars from B to the arms of 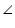 A (see the given figure). Show that:
A (see the given figure). Show that:
(i) 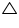 APB
APB 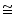
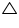 AQB
AQB
(ii) BP = BQ or B is equidistant from the arms of 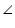 A.
A. 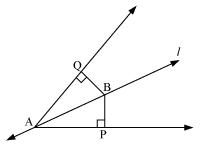
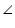 A and B is any point on l. BP and BQ are perpendiculars from B to the arms of
A and B is any point on l. BP and BQ are perpendiculars from B to the arms of 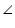 A (see the given figure). Show that:
A (see the given figure). Show that:(i)
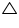 APB
APB 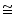
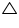 AQB
AQB(ii) BP = BQ or B is equidistant from the arms of
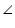 A.
A. 
Solution 5

Question 6
In the given figure, AC = AE, AB = AD and  BAD =
BAD =  EAC. Show that BC = DE.
EAC. Show that BC = DE. 
 BAD =
BAD =  EAC. Show that BC = DE.
EAC. Show that BC = DE. 
Solution 6
Given that  BAD =
BAD =  EAC
EAC
 BAD +
BAD +  DAC =
DAC =  EAC +
EAC +  DAC
DAC
 BAC =
BAC =  DAE
DAE
Now in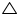 BAC and
BAC and 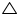 DAE
DAE
AB = AD (given)
 BAC =
BAC =  DAE (proved above)
DAE (proved above)
AC = AE (given)
 BAD =
BAD =  EAC
EAC  BAD +
BAD +  DAC =
DAC =  EAC +
EAC +  DAC
DAC BAC =
BAC =  DAE
DAE Now in
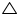 BAC and
BAC and 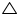 DAE
DAEAB = AD (given)
 BAC =
BAC =  DAE (proved above)
DAE (proved above)AC = AE (given)
Question 7
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that  BAD =
BAD =  ABE and
ABE and  EPA =
EPA =  DPB (See the given figure). Show that
DPB (See the given figure). Show that
(i) 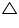 DAP
DAP 
 EBP
EBP
(ii) AD = BE 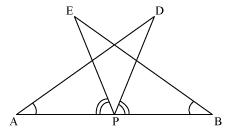
 BAD =
BAD =  ABE and
ABE and  EPA =
EPA =  DPB (See the given figure). Show that
DPB (See the given figure). Show that (i)
 DAP
DAP 
 EBP
EBP(ii) AD = BE

Solution 7
Given that  EPA =
EPA =  DPB
DPB 
 EPA +
EPA +  DPE =
DPE =  DPB +
DPB +  DPE
DPE
 DPA =
DPA =  EPB
EPB
Now in DAP and
DAP and  EBP
EBP
 DAP =
DAP =  EBP (given)
EBP (given)
AP = BP (P is mid point of AB)
 DPA =
DPA =  EPB (from above)
EPB (from above) 
 EPA =
EPA =  DPB
DPB 
 EPA +
EPA +  DPE =
DPE =  DPB +
DPB +  DPE
DPE
 DPA =
DPA =  EPB
EPB Now in
 DAP and
DAP and 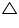 EBP
EBP DAP =
DAP =  EBP (given)
EBP (given)AP = BP (P is mid point of AB)
 DPA =
DPA =  EPB (from above)
EPB (from above)
Question 8
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
(i)  AMC
AMC 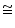
 BMD
BMD
(ii)  DBC is a right angle.
DBC is a right angle.
(iii)  DBC
DBC 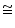
 ACB
ACB
(iv) CM = 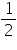 AB
AB 
(i)
 AMC
AMC 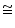
 BMD
BMD(ii)
 DBC is a right angle.
DBC is a right angle.(iii)
 DBC
DBC 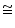
 ACB
ACB(iv) CM =
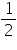 AB
AB 
Solution 8
(i) In  AMC and
AMC and  BMD
BMD
AM = BM (M is mid point of AB)
 AMC =
AMC =  BMD (vertically opposite angles)
BMD (vertically opposite angles)
CM = DM (given)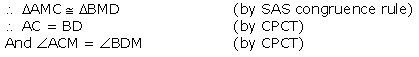 (ii) We have
(ii) We have  ACM =
ACM =  BDM
BDM
But ACM and
ACM and  BDM are alternate interior angles
BDM are alternate interior angles
Since alternate angles are equal.
Hence, we can say that DB || AC
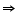
 DBC +
DBC +  ACB = 180o (co-interior angles)
ACB = 180o (co-interior angles)  DBC + 90o = 180o
DBC + 90o = 180o
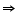
 DBC + 90o = 1800
DBC + 90o = 1800 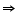
 DBC = 90o (iii) Now in
DBC = 90o (iii) Now in  DBC and
DBC and  ACB
ACB
DB = AC (Already proved)
 DBC =
DBC =  ACB (each 90o )
ACB (each 90o )
BC = CB (Common) (iv) We have
(iv) We have  DBC
DBC 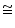
 ACB
ACB 
 AMC and
AMC and  BMD
BMDAM = BM (M is mid point of AB)
 AMC =
AMC =  BMD (vertically opposite angles)
BMD (vertically opposite angles)CM = DM (given)
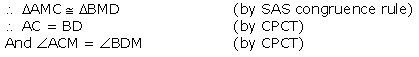 (ii) We have
(ii) We have  ACM =
ACM =  BDM
BDMBut
 ACM and
ACM and  BDM are alternate interior angles
BDM are alternate interior anglesSince alternate angles are equal.
Hence, we can say that DB || AC
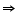
 DBC +
DBC +  ACB = 180o (co-interior angles)
ACB = 180o (co-interior angles)  DBC + 90o = 180o
DBC + 90o = 180o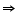
 DBC + 90o = 1800
DBC + 90o = 1800 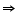
 DBC = 90o (iii) Now in
DBC = 90o (iii) Now in  DBC and
DBC and  ACB
ACBDB = AC (Already proved)
 DBC =
DBC =  ACB (each 90o )
ACB (each 90o )BC = CB (Common)
 DBC
DBC 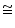
 ACB
ACB 
NCERT Solution for Class 9 Mathematics Chapter 7 - Triangles Page/Excercise 7.2
Question 1
In an isosceles triangle ABC, with AB = AC, the bisectors of 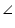 B and
B and 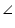 C intersect each other at O. Join A to O. Show that:
C intersect each other at O. Join A to O. Show that:
(i) OB = OC (ii) AO bisects 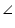 A
A
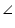 B and
B and 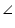 C intersect each other at O. Join A to O. Show that:
C intersect each other at O. Join A to O. Show that: (i) OB = OC (ii) AO bisects
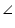 A
A
Solution 1
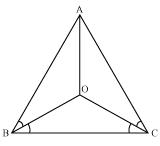 (i) It is given that in triangle ABC, AC = AB
(i) It is given that in triangle ABC, AC = AB 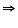
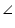 ACB =
ACB = 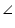 ABC (angles opposite to equal sides of a triangle are equal)
ABC (angles opposite to equal sides of a triangle are equal) 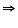
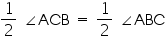
 OBC =
OBC =  OBC
OBC 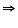 OB = OC (sides opposite to equal angles of a triangle are also equal) (ii) Now in
OB = OC (sides opposite to equal angles of a triangle are also equal) (ii) Now in 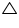 OAB and
OAB and 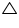 OAC
OACAO =AO (common)
AB = AC (given)
OB = OC (proved above)
So,
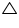 OAB
OAB 
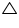 OAC (by SSS congruence rule)
OAC (by SSS congruence rule) 
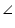 BAO =
BAO = 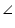 CAO (C.P.C.T.)
CAO (C.P.C.T.)
Question 2
In  ABC, AD is the perpendicular bisector of BC (see the given figure). Show that
ABC, AD is the perpendicular bisector of BC (see the given figure). Show that  ABC is an isosceles triangle in which AB = AC.
ABC is an isosceles triangle in which AB = AC.
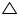 ABC, AD is the perpendicular bisector of BC (see the given figure). Show that
ABC, AD is the perpendicular bisector of BC (see the given figure). Show that 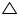 ABC is an isosceles triangle in which AB = AC.
ABC is an isosceles triangle in which AB = AC.
Solution 2
In 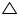 ADC and
ADC and 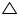 ADB
ADB
AD = AD (Common)
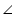 ADC =
ADC = ADB (each 90o)
ADB (each 90o)
CD = BD (AD is the perpendicular bisector of BC)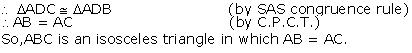
 ADC and
ADC and 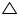 ADB
ADBAD = AD (Common)
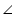 ADC =
ADC =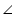 ADB (each 90o)
ADB (each 90o)CD = BD (AD is the perpendicular bisector of BC)
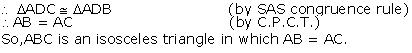
Question 3
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.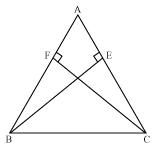

Solution 3
In  AEB and
AEB and  AFC
AFC
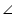 AEB =
AEB = 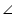 AFC (each 90o)
AFC (each 90o)
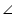 A =
A = 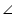 A (common angle)
A (common angle)
AB = AC (given)
 AEB and
AEB and  AFC
AFC 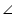 AEB =
AEB = 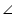 AFC (each 90o)
AFC (each 90o)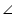 A =
A = 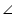 A (common angle)
A (common angle)AB = AC (given)
Question 4
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure) show that
(i)  ABE
ABE 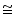
 ACF
ACF
(ii) AB = AC, i.e., ABC is an isosceles triangle. 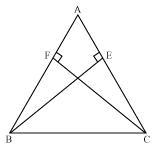
(i)
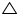 ABE
ABE 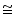
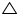 ACF
ACF (ii) AB = AC, i.e., ABC is an isosceles triangle.

Solution 4
(i) In 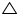 AEB and
AEB and 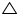 AFC
AFC
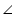 AEB =
AEB = 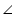 AFC (each 90�)
AFC (each 90�)
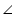 A =
A = 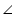 A (common angle)
A (common angle)
BE = CF (given)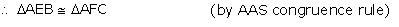 (ii) We have already proved
(ii) We have already proved
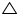 AEB
AEB 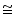
 AFC
AFC
 AB = AC (by CPCT)
AB = AC (by CPCT)
 AEB and
AEB and  AFC
AFC 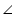 AEB =
AEB = 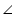 AFC (each 90�)
AFC (each 90�)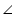 A =
A = 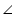 A (common angle)
A (common angle)BE = CF (given)
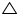 AEB
AEB 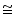
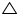 AFC
AFC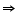 AB = AC (by CPCT)
AB = AC (by CPCT)
Question 5
ABC and DBC are two isosceles triangles on the same base BC (see the given figure). Show that  ABD =
ABD =  ACD.
ACD.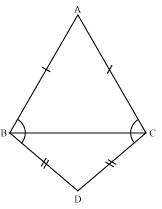
 ABD =
ABD = 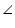 ACD.
ACD.
Solution 5
 Let us join AD
Let us join ADIn
 ABD and
ABD and  ACD
ACDAB = AC (Given)
BD = CD (Given)
AD = AD (Common side)
Question 6
 ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that
ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that  BCD is a right angle.
BCD is a right angle.
 ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that
ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see the given figure). Show that  BCD is a right angle.
BCD is a right angle.
Solution 6
In  ABC
ABC
AB = AC (given)
 ACB =
ACB =  ABC (angles opposite to equal sides of a triangle are also equal)
ABC (angles opposite to equal sides of a triangle are also equal)
Now In ACD
ACD
AC = AD
 ADC =
ADC =  ACD (angles opposite to equal sides of a triangle are also equal)
ACD (angles opposite to equal sides of a triangle are also equal)
Now, in BCD
BCD
 ABC +
ABC +  BCD +
BCD +  ADC = 180o (angle sum property of a triangle)
ADC = 180o (angle sum property of a triangle)
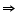
 ACB +
ACB +  ACB +
ACB + ACD +
ACD +  ACD = 180o
ACD = 180o
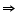 2(
2( ACB +
ACB +  ACD) = 180o
ACD) = 180o
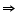 2(
2( BCD) = 180o
BCD) = 180o
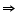
 BCD = 90o
BCD = 90o
 ABC
ABC AB = AC (given)
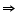
 ACB =
ACB =  ABC (angles opposite to equal sides of a triangle are also equal)
ABC (angles opposite to equal sides of a triangle are also equal)Now In
 ACD
ACDAC = AD
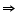
 ADC =
ADC =  ACD (angles opposite to equal sides of a triangle are also equal)
ACD (angles opposite to equal sides of a triangle are also equal)Now, in
 BCD
BCD  ABC +
ABC +  BCD +
BCD +  ADC = 180o (angle sum property of a triangle)
ADC = 180o (angle sum property of a triangle)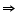
 ACB +
ACB +  ACB +
ACB + ACD +
ACD +  ACD = 180o
ACD = 180o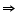 2(
2( ACB +
ACB +  ACD) = 180o
ACD) = 180o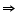 2(
2( BCD) = 180o
BCD) = 180o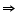
 BCD = 90o
BCD = 90o
Question 7
ABC is a right angled triangle in which 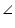 A = 90o and AB = AC. Find
A = 90o and AB = AC. Find 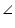 B and
B and 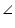 C.
C.
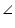 A = 90o and AB = AC. Find
A = 90o and AB = AC. Find 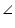 B and
B and 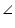 C.
C.
Solution 7
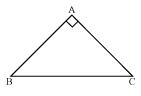 Given that AB = AC
Given that AB = AC 
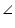 C =
C = 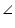 B (angles opposite to equal sides are also equal) In
B (angles opposite to equal sides are also equal) In 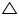 ABC,
ABC, 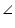 A +
A + 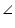 B +
B + 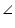 C = 180o (angle sum property of a triangle)
C = 180o (angle sum property of a triangle)  90o +
90o + 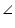 B +
B + 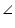 C = 180o
C = 180o  90o +
90o + 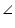 B +
B + 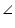 B = 180o
B = 180o 2
2 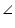 B = 90o
B = 90o
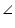 B = 45�
B = 45�
Question 8
Show that the angles of an equilateral triangle are 60o each.
Solution 8
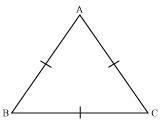 Let us consider that ABC is an equilateral triangle.
Let us consider that ABC is an equilateral triangle.So, AB = BC = AC
Now, AB = AC
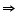
 C =
C = 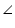 B (angles opposite to equal sides of a triangle are equal)
B (angles opposite to equal sides of a triangle are equal)We also have
AC = BC
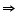
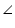 B =
B = 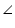 A (angles opposite to equal sides of a triangle are equal)
A (angles opposite to equal sides of a triangle are equal)So, we have
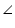 A =
A = 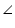 B =
B = 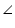 C
CNow, in
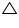 ABC
ABC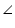 A +
A + 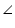 B +
B + 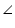 C = 180o
C = 180o 
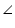 A +
A + 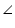 A +
A + 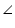 A = 180o
A = 180o  3
3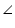 A = 180o
A = 180o 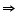
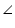 A = 60o
A = 60o 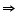
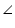 A =
A = 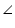 B =
B = 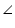 C = 60o
C = 60o Hence, in an equilateral triangle all interior angles are of 60o.
NCERT Solution for Class 9 Mathematics Chapter 7 - Triangles Page/Excercise 7.3
Question 1
 ABC and
ABC and  DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see the given figure). If AD is extended to intersect BC at P, show that
DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see the given figure). If AD is extended to intersect BC at P, show that
(i)  ABD
ABD 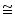
 ACD
ACD
(ii)  ABP
ABP 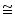
 ACP
ACP
(iii) AP bisects  A as well as
A as well as  D.
D.
(iv) AP is the perpendicular bisector of BC. 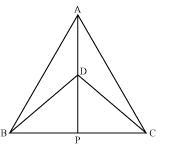
 ABC and
ABC and  DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see the given figure). If AD is extended to intersect BC at P, show that
DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see the given figure). If AD is extended to intersect BC at P, show that (i)
 ABD
ABD 
 ACD
ACD(ii)
 ABP
ABP 
 ACP
ACP (iii) AP bisects
 A as well as
A as well as  D.
D.(iv) AP is the perpendicular bisector of BC.

Solution 1
(i) In  ABD and
ABD and  ACD
ACD
AB = AC (given)
BD = CD (given)
AD = AD (common)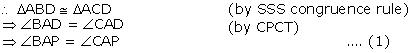 (ii) In
(ii) In  ABP and
ABP and  ACP
ACP
AB = AC (given).
 BAP =
BAP =  CAP [from equation (1)]
CAP [from equation (1)]
AP = AP (common) (iii) From equation (1)
(iii) From equation (1)
 BAP =
BAP =  CAP
CAP
Hence, AP bisect A
A
Now in BDP and
BDP and  CDP
CDP
BD = CD (given)
DP = DP (common)
BP = CP [from equation (2)] (iv) We have
(iv) We have  BDP
BDP 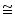
 CDP
CDP 
 ABD and
ABD and  ACD
ACDAB = AC (given)
BD = CD (given)
AD = AD (common)
 (ii) In
(ii) In  ABP and
ABP and  ACP
ACPAB = AC (given).
 BAP =
BAP =  CAP [from equation (1)]
CAP [from equation (1)]AP = AP (common)
 BAP =
BAP =  CAP
CAP Hence, AP bisect
 A
ANow in
 BDP and
BDP and  CDP
CDPBD = CD (given)
DP = DP (common)
BP = CP [from equation (2)]
 (iv) We have
(iv) We have  BDP
BDP 
 CDP
CDP
Now,  BPD +
BPD +  CPD = 180o (linear pair angles)
CPD = 180o (linear pair angles)
 BPD +
BPD +  CPD = 180o (linear pair angles)
CPD = 180o (linear pair angles) BPD +
BPD +  BPD = 180o
BPD = 180o
2 BPD = 180o [from equation (4)]
BPD = 180o [from equation (4)]
 BPD = 180o [from equation (4)]
BPD = 180o [from equation (4)] BPD = 90o ...(5)
BPD = 90o ...(5)
From equations (2) and (5), we can say that AP is perpendicular bisector of BC.
Question 2
AD is an altitude of an isosceles triangles ABC in which AB = AC. Show that (i) AD bisects BC (ii) AD bisects  A.
A.
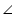 A.
A.
Solution 2
 (i) In
(i) In  BAD and
BAD and 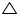 CAD
CAD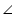 ADB =
ADB = 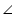 ADC (each 90o as AD is an altitude)
ADC (each 90o as AD is an altitude)AB = AC (given)
AD = AD (common)
 (ii) Also by CPCT,
(ii) Also by CPCT, 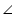 BAD =
BAD = 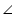 CAD
CADHence, AD bisects
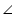 A.
A.
(ii) Also by CPCT,
ÐBAD = ÐCAD
Hence, AD bisects ÐA.
Question 3
Two side AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of  PQR (see the given figure). Show that:
PQR (see the given figure). Show that:
(i)  ABM
ABM 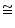
 PQN
PQN
(ii)  ABC
ABC 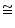
 PQR
PQR 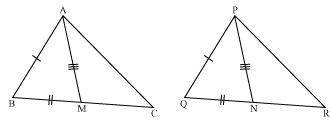
 PQR (see the given figure). Show that:
PQR (see the given figure). Show that: (i)
 ABM
ABM 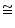
 PQN
PQN(ii)
 ABC
ABC 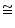
 PQR
PQR 
Solution 3
(i) In  ABC, AM is median to BC
ABC, AM is median to BC 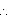 BM =
BM =  BC In
BC In  PQR, PN is median to QR
PQR, PN is median to QR 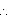 QN =
QN = 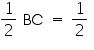 QR But BC = QR
QR But BC = QR 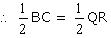
 BN = QN ...(i) Now, in
BN = QN ...(i) Now, in  ABM and
ABM and  PQN
PQN
AB = PQ (given)
BM = QN [from equation (1)]
AM = PN (given)
 (ii) Now in
(ii) Now in  ABC and
ABC and  PQR
PQR
AB = PQ (given)
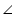 ABC =
ABC = 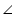 PQR [from equation (2)]
PQR [from equation (2)]
BC = QR (given)
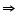
 ABC
ABC 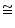
 PQR (by SAS congruence rule)
PQR (by SAS congruence rule)
 ABC, AM is median to BC
ABC, AM is median to BC  BC In
BC In  PQR, PN is median to QR
PQR, PN is median to QR 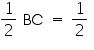 QR But BC = QR
QR But BC = QR 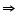 BN = QN ...(i) Now, in
BN = QN ...(i) Now, in  ABM and
ABM and  PQN
PQNAB = PQ (given)
BM = QN [from equation (1)]
AM = PN (given)
 (ii) Now in
(ii) Now in  ABC and
ABC and  PQR
PQR AB = PQ (given)
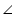 ABC =
ABC = 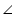 PQR [from equation (2)]
PQR [from equation (2)]BC = QR (given)
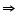
 ABC
ABC 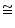
 PQR (by SAS congruence rule)
PQR (by SAS congruence rule)
Question 4
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Solution 4
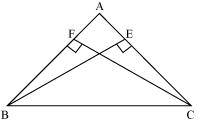 In
In 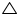 BEC and
BEC and 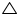 CFB
CFB 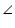 BEC =
BEC = 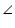 CFB (each 90o )
CFB (each 90o )BC = CB (common)
BE = CF (given)
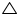 ABC is isosceles.
ABC is isosceles.
Question 5
ABC is an isosceles triangle with AB = AC. Drawn AP 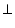 BC to show that
BC to show that 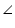 B =
B = 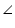 C.
C.
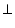 BC to show that
BC to show that  B =
B =  C.
C.
Solution 5
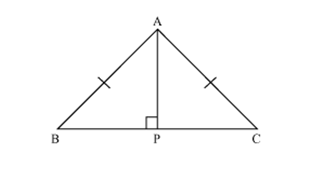 In
In  APB and
APB and 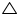 APC
APC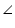 APB =
APB = 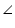 APC (each 90o)
APC (each 90o)AB =AC (given)
AP = AP
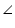 B =
B = 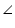 C (by using CPCT)
C (by using CPCT)NCERT Solution for Class 9 Mathematics Chapter 7 - Triangles Page/Excercise 7.4
Question 1
Show that in a right angled triangle, the hypotenuse is the longest side.
Solution 1
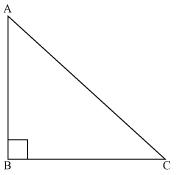 Let us consider a right angled triangle ABC, right angle at B.
Let us consider a right angled triangle ABC, right angle at B. In
 ABC
ABC A +
A + 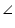 B +
B + 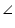 C = 180o (angle sum property of a triangle)
C = 180o (angle sum property of a triangle) 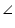 A + 90o +
A + 90o + 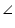 C = 180o
C = 180o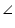 A +
A + 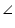 C = 90o
C = 90oHence, the other two angles have to be acute (i.e. less than 90�).
 [In any triangle, the side opposite to the larger (greater) angle is longer]
[In any triangle, the side opposite to the larger (greater) angle is longer]So, AC is the largest side in
 ABC.
ABC.But AC is the hypotenuse of
 ABC. Therefore, hypotenuse is the longest side in a right angled triangle.
ABC. Therefore, hypotenuse is the longest side in a right angled triangle.
Question 2
In the given figure sides AB and AC of 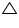 ABC are extended to points P and Q respectively. Also,
ABC are extended to points P and Q respectively. Also,  PBC
PBC 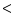
 QCB. Show that AC > AB.
QCB. Show that AC > AB.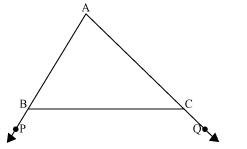
 ABC are extended to points P and Q respectively. Also,
ABC are extended to points P and Q respectively. Also,  PBC
PBC 
 QCB. Show that AC > AB.
QCB. Show that AC > AB.
Solution 2
In the given figure,
 ABC +
ABC +  PBC = 180p (linear pair)
PBC = 180p (linear pair)
 ABC = 180o -
ABC = 180o -  PBC ... (1)
PBC ... (1)
Also,
 ACB +
ACB +  QCB = 180o
QCB = 180o
 ACB = 180o -
ACB = 180o -  QCB ... (2)
QCB ... (2)
As PBC <
PBC <  QCB
QCB
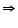 180� -
180� -  PBC > 180o -
PBC > 180o -  QCB.
QCB.
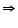
 ABC >
ABC >  ACB [From equations (1) and (2)]
ACB [From equations (1) and (2)]
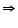 AC > AB (side opposite to larger angle is larger)
AC > AB (side opposite to larger angle is larger)
 ABC +
ABC +  PBC = 180p (linear pair)
PBC = 180p (linear pair)
 ABC = 180o -
ABC = 180o -  PBC ... (1)
PBC ... (1)Also,
 ACB +
ACB +  QCB = 180o
QCB = 180o ACB = 180o -
ACB = 180o -  QCB ... (2)
QCB ... (2)As
 PBC <
PBC <  QCB
QCB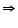 180� -
180� -  PBC > 180o -
PBC > 180o -  QCB.
QCB.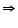
 ABC >
ABC >  ACB [From equations (1) and (2)]
ACB [From equations (1) and (2)]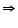 AC > AB (side opposite to larger angle is larger)
AC > AB (side opposite to larger angle is larger)
Question 3
In the given figure, 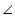 B <
B < 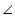 A and
A and 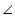 C <
C < 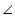 D. Show that AD < BC.
D. Show that AD < BC.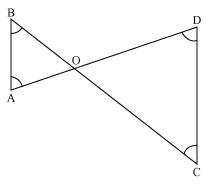
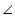 B <
B < 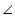 A and
A and 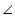 C <
C < 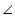 D. Show that AD < BC.
D. Show that AD < BC.
Solution 3
In 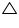 AOB
AOB
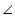 B <
B < 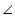 A
A
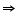 AO < BO (side opposite to smaller angle is smaller) ... (1)
AO < BO (side opposite to smaller angle is smaller) ... (1)
Now in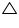 COD
COD
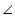 C <
C < 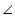 D
D
 OD < OC (side opposite to smaller angle is smaller) ... (2)
OD < OC (side opposite to smaller angle is smaller) ... (2)
On adding equations (1) and (2), we have
AO + OD < BO + OC
AD < BC
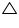 AOB
AOB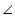 B <
B < 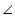 A
A AO < BO (side opposite to smaller angle is smaller) ... (1)
AO < BO (side opposite to smaller angle is smaller) ... (1)Now in
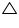 COD
COD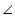 C <
C < 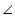 D
D OD < OC (side opposite to smaller angle is smaller) ... (2)
OD < OC (side opposite to smaller angle is smaller) ... (2)On adding equations (1) and (2), we have
AO + OD < BO + OC
AD < BC
Question 4
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that  A >
A >  C and
C and  B >
B >  D.
D.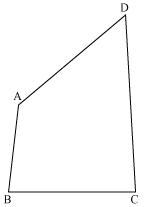
 A >
A >  C and
C and  B >
B >  D.
D.
Solution 4
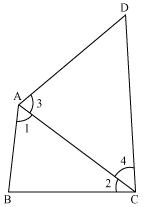 Let us join AC.
Let us join AC.In
 ABC
ABCAB < BC (AB is smallest side of quadrilateral ABCD)
 ADC
ADCAD < CD (CD is the largest side of quadrilateral ABCD)
 2 +
2 +  4 <
4 <  1 +
1 +  3
3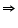
 C <
C <  A
A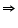
 A >
A >  C
CLet us join BD.
 In
In  ABD
ABDAB < AD (AB is smallest side of quadrilateral ABCD)
 BDC
BDCBC < CD (CD is the largest side of quadrilateral ABCD)
 8 +
8 +  7 <
7 <  5 +
5 +  6
6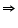
 D <
D <  B
B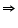
 B >
B >  D
D
Question 5
In the given figure, PR > PQ and PS bisects 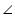 QPR. Prove that
QPR. Prove that 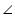 PSR >
PSR >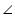 PSQ.
PSQ.
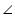 QPR. Prove that
QPR. Prove that 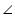 PSR >
PSR >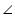 PSQ.
PSQ.
Solution 5
As PR > PQ 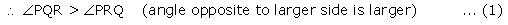 PS is the bisector of
PS is the bisector of  QPR
QPR 

 QPR
QPR 
Question 6
Show that of all line segments drawn form a given point not on it, the perpendicular line segment is the shortest.
Solution 6
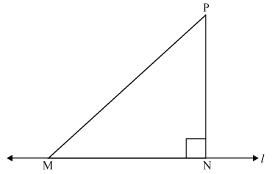 Let us take a line l and from point P (i.e. not on line l) we have drawn two line segments PN and PM. Let PN be perpendicular to line l and PM is drawn at some other angle.
Let us take a line l and from point P (i.e. not on line l) we have drawn two line segments PN and PM. Let PN be perpendicular to line l and PM is drawn at some other angle.In
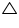 PNM
PNM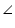 N = 90o
N = 90oNow,
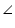 P +
P + 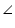 N +
N + 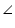 M = 180o (Angle sum property of a triangle)
M = 180o (Angle sum property of a triangle) 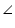 P +
P + 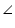 M = 90o
M = 90o Clearly,
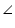 M is an acute angle
M is an acute angle 
NCERT Solution for Class 9 Mathematics Chapter 7 - Triangles Page/Excercise 7.5
Question 1
ABC is a triangle. Locate a point in the interior of 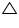 ABC which is equidistant from all the vertices of
ABC which is equidistant from all the vertices of 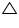 ABC.
ABC.
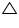 ABC which is equidistant from all the vertices of
ABC which is equidistant from all the vertices of 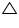 ABC.
ABC.
Solution 1
Circumcentre of a triangle is always equidistant from all the vertices of that triangle. Circumcentre is the point where perpendicular bisectors, of all the sides of triangles meet together.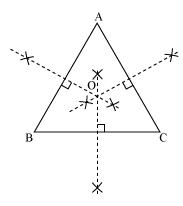 As here in
As here in 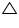 ABC we can find the circumcentre by drawing the perpendicular bisectors of sides AB, BC, and CA of this triangle. O is the point where these bisectors are meeting together. So O is point which is equidistant from all the vertices of
ABC we can find the circumcentre by drawing the perpendicular bisectors of sides AB, BC, and CA of this triangle. O is the point where these bisectors are meeting together. So O is point which is equidistant from all the vertices of 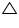 ABC.
ABC.
 As here in
As here in 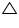 ABC we can find the circumcentre by drawing the perpendicular bisectors of sides AB, BC, and CA of this triangle. O is the point where these bisectors are meeting together. So O is point which is equidistant from all the vertices of
ABC we can find the circumcentre by drawing the perpendicular bisectors of sides AB, BC, and CA of this triangle. O is the point where these bisectors are meeting together. So O is point which is equidistant from all the vertices of  ABC.
ABC.
Question 2
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
Solution 2
The point which is equidistant from all the sides of a triangle is incenter of triangle. Incentre of triangle is the intersection point of angle bisectors of interior angles of that triangle. Here in
Here in 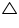 ABC we can find the incentre of this triangle by drawing the angle bisectors of interior angles of this triangle. I is the point where these angle bisectors are intersecting each other. So, I is the point, equidistant from all the sides of
ABC we can find the incentre of this triangle by drawing the angle bisectors of interior angles of this triangle. I is the point where these angle bisectors are intersecting each other. So, I is the point, equidistant from all the sides of  ABC.
ABC.
 Here in
Here in  ABC we can find the incentre of this triangle by drawing the angle bisectors of interior angles of this triangle. I is the point where these angle bisectors are intersecting each other. So, I is the point, equidistant from all the sides of
ABC we can find the incentre of this triangle by drawing the angle bisectors of interior angles of this triangle. I is the point where these angle bisectors are intersecting each other. So, I is the point, equidistant from all the sides of  ABC.
ABC.
Question 3
In a huge park people are concentrated at three points (see the given figure) 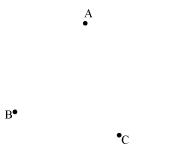 A: where there are different slides and swings for children,
A: where there are different slides and swings for children,
B: near which a man-made lake is situated, C: which is near to a large parking and exit. Where should an icecream parlour be set up so that maximum number of persons can approach it?
(Hint: The parlor should be equidistant from A, B and C)
 A: where there are different slides and swings for children,
A: where there are different slides and swings for children,B: near which a man-made lake is situated, C: which is near to a large parking and exit. Where should an icecream parlour be set up so that maximum number of persons can approach it?
(Hint: The parlor should be equidistant from A, B and C)
Solution 3
Ice-cream parlour should be set up at the circumcentre O of  ABC.
ABC. 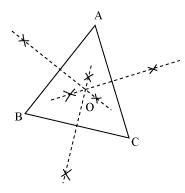 In this situation maximum number of persons can approach to it. We can find circumcentre O of this triangle by drawing perpendicular bisectors of the sides of this triangle.
In this situation maximum number of persons can approach to it. We can find circumcentre O of this triangle by drawing perpendicular bisectors of the sides of this triangle.
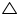 ABC.
ABC.  In this situation maximum number of persons can approach to it. We can find circumcentre O of this triangle by drawing perpendicular bisectors of the sides of this triangle.
In this situation maximum number of persons can approach to it. We can find circumcentre O of this triangle by drawing perpendicular bisectors of the sides of this triangle.
Question 4
Complete the hexagonal and star shaped Rangolies (see the given figures) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles? 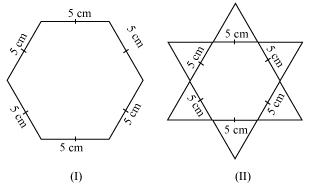

Solution 4
We may observe that hexagonal shaped rangoly is having 6 equilateral triangles in it. Area of
Area of  OAB =
OAB = 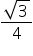 (side)2 =
(side)2 = 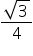 (5)2
(5)2 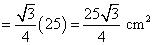
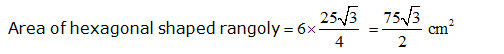
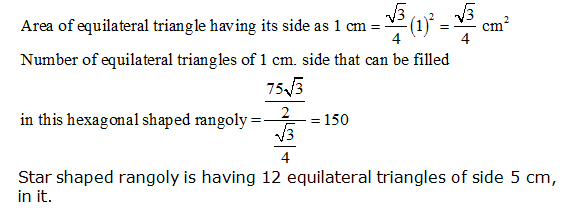
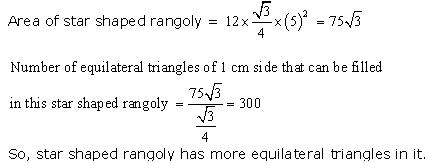
 Area of
Area of  OAB =
OAB = 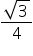 (side)2 =
(side)2 = 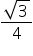 (5)2
(5)2 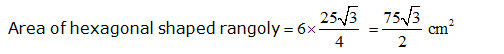
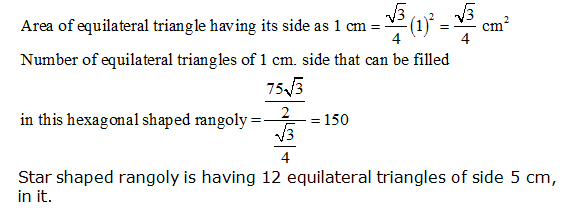

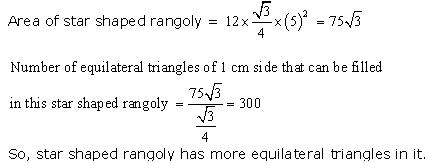
No comments:
Post a Comment