NCERT Solution for Class 9 Mathematics Chapter 2 - Polynomials Page/Excercise 2.1
Question 1
Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer 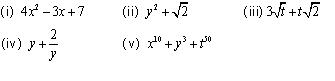
Solution 1
(i) 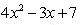
Yes, this expression is a polynomial in one variable x.
(ii) 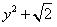
Yes, this expression is a polynomial in one variable y.
(iii) 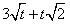
No, here the exponent of variable t in term 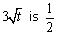 which is not a whole number.
which is not a whole number.
So this expression is not a polynomial.
(iv) 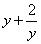
No, here the exponent of variable t in term 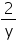 is -1, which is not a whole number. So this expression is not a polynomial.
is -1, which is not a whole number. So this expression is not a polynomial.
(v) 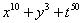
No, this expression is a polynomial in 3 variables x, y and t.
Concept Insight: In such problems to check whether the given algebraic expressions is a polynomial or not, check the exponents of variable to be a whole number. The second step is to look for the number of variables the expression has. Any alphabet used in the expression is the variable unless specified as constant.
Question 2
Write the coefficient of x2 in each of the following: 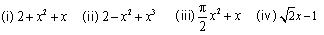
Solution 2
(i) 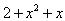 In the above expression coefficient of x2 is 1 (ii)
In the above expression coefficient of x2 is 1 (ii)  In the above expression coefficient of x2 is - 1. (iii)
In the above expression coefficient of x2 is - 1. (iii) 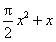 In the above expression coefficient of
In the above expression coefficient of 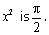 (iv)
(iv) 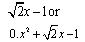 In the above expression coefficient of x2 is 0. Concept Insight: The constant/ variable multiplied with the variable is the coefficient of the variable. Also consider the sign (+ve or the -ve) of the term while writing the coefficient.
In the above expression coefficient of x2 is 0. Concept Insight: The constant/ variable multiplied with the variable is the coefficient of the variable. Also consider the sign (+ve or the -ve) of the term while writing the coefficient.
Question 3
Give one example each of a binomial of degree 35, and of a monomial of degree 100.
Solution 3
Degree of a polynomial is the highest power of variable in the polynomial.Binomial has two terms in it. So binomial of degree 35 can be written as x35 + 7 . Monomial has only one term in it. So monomial of degree 100 can be written as 7x100. Concept Insight: Mono, bi and tri means one, two and three respectively. So, monomial is a polynomial having one term similarly for binomials and trinomials. Degree is the highest exponent of variable. The answer is not unique in such problems . Remember that the terms are always separated by +ve or -ve sign and not with .
Question 4
Write the degree of each of the following polynomials: 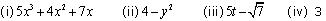
Solution 4
Degree of a polynomial is the highest power of variable in the polynomial. 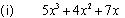 This is a polynomial in variable x and highest power of variable x is 3. So, degree of this polynomial is 3
This is a polynomial in variable x and highest power of variable x is 3. So, degree of this polynomial is 3 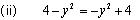 This is a polynomial in variable y and the highest power of variable y is 2. So degree of this polynomial is 2.
This is a polynomial in variable y and the highest power of variable y is 2. So degree of this polynomial is 2. 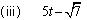 This is a polynomial in variable t and the highest power of variable t is 1. So degree of this polynomial is 1. (iv) 3 This is a constant polynomial. Degree of a constant polynomial is always 0. Concept Insight: Degree is the highest exponent of the variable. While finding the degree of a polynomial express the polynomial in standard form Combine the like terms and Remember the result that xo = 1.
This is a polynomial in variable t and the highest power of variable t is 1. So degree of this polynomial is 1. (iv) 3 This is a constant polynomial. Degree of a constant polynomial is always 0. Concept Insight: Degree is the highest exponent of the variable. While finding the degree of a polynomial express the polynomial in standard form Combine the like terms and Remember the result that xo = 1.
Question 5
Classify the following as linear, quadratic and cubic polynomial: 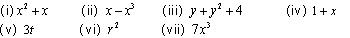
Solution 5
(i) 2 + x2 + x is a quadratic polynomial as its degree is 2.
(ii) x - x3 is a cubic polynomial as its degree is 3.
(iii) y + y2 + 4 is a quadratic polynomial as its degree is 2.
(iv) 1 + x is a linear polynomial as its degree is 1.
(v) 3t is a linear polynomial as its degree is 1.
(vi) r2 is a quadratic polynomial as its degree is 2.
(vii) 7x3 is a cubic polynomial as its degree is 3. Concept Insight: Linear polynomial, quadratic polynomial and cubic polynomial has its degrees as 1, 2, and 3 respectively.
(ii) x - x3 is a cubic polynomial as its degree is 3.
(iii) y + y2 + 4 is a quadratic polynomial as its degree is 2.
(iv) 1 + x is a linear polynomial as its degree is 1.
(v) 3t is a linear polynomial as its degree is 1.
(vi) r2 is a quadratic polynomial as its degree is 2.
(vii) 7x3 is a cubic polynomial as its degree is 3. Concept Insight: Linear polynomial, quadratic polynomial and cubic polynomial has its degrees as 1, 2, and 3 respectively.
NCERT Solution for Class 9 Mathematics Chapter 2 - Polynomials Page/Excercise 2.2
Question 1
Find the value of the polynomial 5x - 4x2 +3 at
(i) x = 0 (ii) x = - 1 (iii) x = 2
(i) x = 0 (ii) x = - 1 (iii) x = 2
Solution 1
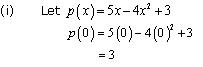
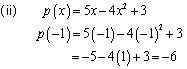
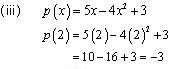 Concept Insight: Given Polynomial is p(x) to find the value of given polynomial at any particular value of x replace the variable x with its corresponding value. Remember for odd power of negative number the negative sign remains while for even power of negative numbers the negative sign vanishes. Also check for calculation errors; there are chances of making calculation mistake while computing square, cubes and higher powers of numbers.
Concept Insight: Given Polynomial is p(x) to find the value of given polynomial at any particular value of x replace the variable x with its corresponding value. Remember for odd power of negative number the negative sign remains while for even power of negative numbers the negative sign vanishes. Also check for calculation errors; there are chances of making calculation mistake while computing square, cubes and higher powers of numbers.
Question 2
Find p(0), p(1) and p(2) for each of the following polynomials:
(i) p(y) = y2 - y + 1 (ii) p(t) = 2 + t + 2t2 - t3
(iii) p(x) = x3 (iv) p(x) = (x - 1) (x + 1)
(i) p(y) = y2 - y + 1 (ii) p(t) = 2 + t + 2t2 - t3
(iii) p(x) = x3 (iv) p(x) = (x - 1) (x + 1)
Solution 2
(i) p(y) = y2 - y + 1
p(0) = (0)2 - (0) + 1 = 1
p(1) = (1)2 - (1) + 1 = 1
p(2) = (2)2 - (2) + 1 = 3 (ii) p(t) = 2 + t + 2t2 - t3
p(0) = 2 + 0 + 2 (0)2 - (0)3 = 2
p(1) = 2 + (1) + 2(1)2 - (1)3
= 2 + 1 + 2 - 1 = 4 p(2) = 2 + 2 + 2(2)2 - (2)3
= 2 + 2 + 8 - 8 = 4 (iii) p(x) = x3
p(0) = (0)3 = 0
p(1) = (1)3 = 1
p(2) = (2)3 = 8 (iv) p(x) = (x - 1) (x + 1)
p(0) = (0 - 1) (0 + 1) = (- 1) (1) = - 1
p(1) = (1 - 1) (1 + 1) = 0 (2) = 0
p(2) = (2 - 1 ) (2 + 1) = 1(3) = 3 Concept Insight: Replace the variable with 0, 1 or 2 in the given polynomials to obtain the required value. Be careful about the calculations, there are chances of making calculation mistake while computing square, cubes and higher powers of numbers. Carefully apply the properties of addition, subtraction and multiplication of numbers. While multiplying two binomials multiply each term of the binomial to each term of the other binomial.
p(0) = (0)2 - (0) + 1 = 1
p(1) = (1)2 - (1) + 1 = 1
p(2) = (2)2 - (2) + 1 = 3 (ii) p(t) = 2 + t + 2t2 - t3
p(0) = 2 + 0 + 2 (0)2 - (0)3 = 2
p(1) = 2 + (1) + 2(1)2 - (1)3
= 2 + 1 + 2 - 1 = 4 p(2) = 2 + 2 + 2(2)2 - (2)3
= 2 + 2 + 8 - 8 = 4 (iii) p(x) = x3
p(0) = (0)3 = 0
p(1) = (1)3 = 1
p(2) = (2)3 = 8 (iv) p(x) = (x - 1) (x + 1)
p(0) = (0 - 1) (0 + 1) = (- 1) (1) = - 1
p(1) = (1 - 1) (1 + 1) = 0 (2) = 0
p(2) = (2 - 1 ) (2 + 1) = 1(3) = 3 Concept Insight: Replace the variable with 0, 1 or 2 in the given polynomials to obtain the required value. Be careful about the calculations, there are chances of making calculation mistake while computing square, cubes and higher powers of numbers. Carefully apply the properties of addition, subtraction and multiplication of numbers. While multiplying two binomials multiply each term of the binomial to each term of the other binomial.
Question 3
Verify whether the following are zeroes of the polynomial, indicated against them. 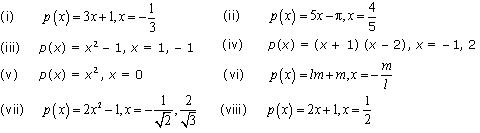
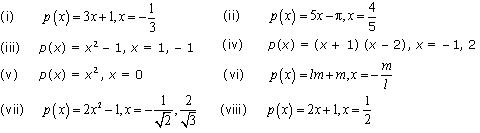
Solution 3
(i) If 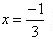 is a zero of given polynomial p(x) = 3x + 1, then
is a zero of given polynomial p(x) = 3x + 1, then  So,
So, 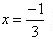 is a zero of given polynomial (ii) If
is a zero of given polynomial (ii) If 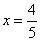 is a zero of polynomial p(x) = 5x -
is a zero of polynomial p(x) = 5x -  , then
, then 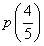 should be 0
should be 0 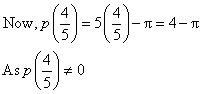 So,
So, 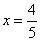 is not a zero of given polynomial (iii) If x = 1 and x = - 1 are zeroes of polynomial p(x) = x2 - 1 then p(1) and p(- 1) should be 0
is not a zero of given polynomial (iii) If x = 1 and x = - 1 are zeroes of polynomial p(x) = x2 - 1 then p(1) and p(- 1) should be 0
Now, p(1) = (1)2 - 1 = 0
p(- 1) = (- 1)2 - 1 = 0
Hence x = 1 and - 1 are zeroes of polynomial. (iv) If x = - 1 and x = 2 are zeroes of polynomial p(x) = (x +1) (x - 2), then p(- 1) and p(2)should be 0.
Now, p(- 1) = (- 1 + 1) (- 1 - 2) = 0 (-3) = 0
p(2) = (2 + 1) (2 - 2 ) = 3 (0) = 0
So, x = - 1 and x = 2 are zeroes of given polynomial. (v) If x = 0 is a zero of polynomial p(x) = x2 then p(0) should be zero.
Now, p(0) = (0)2 = 0
Hence x = 0 is a zero of given polynomial (vi) If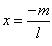 is a zero of polynomial p(x) = lx + m, then
is a zero of polynomial p(x) = lx + m, then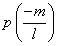 is 0.
is 0.  (vii) If
(vii) If 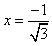 and
and  are zeroes of polynomial p(x) = 3x2 - 1, then
are zeroes of polynomial p(x) = 3x2 - 1, then 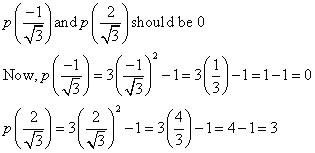 Hence,
Hence, 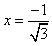 is a zero of given polynomial but
is a zero of given polynomial but  is not a zero of given polynomial. (viii) If
is not a zero of given polynomial. (viii) If  is a zero of polynomial p(x) = 2x + 1 then
is a zero of polynomial p(x) = 2x + 1 then 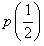 should be 0.
should be 0. 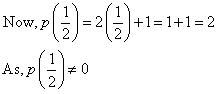 So,
So,  is not a zero of polynomial. Concept Insight: Key idea here is Zero of the polynomial is not the real number zero but it is that value of the variable which makes the value of the polynomial equal to zero. A polynomial can have more than one zeroes.
is not a zero of polynomial. Concept Insight: Key idea here is Zero of the polynomial is not the real number zero but it is that value of the variable which makes the value of the polynomial equal to zero. A polynomial can have more than one zeroes.
 So,
So,  , then
, then 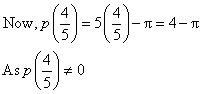 So,
So, Now, p(1) = (1)2 - 1 = 0
p(- 1) = (- 1)2 - 1 = 0
Hence x = 1 and - 1 are zeroes of polynomial. (iv) If x = - 1 and x = 2 are zeroes of polynomial p(x) = (x +1) (x - 2), then p(- 1) and p(2)should be 0.
Now, p(- 1) = (- 1 + 1) (- 1 - 2) = 0 (-3) = 0
p(2) = (2 + 1) (2 - 2 ) = 3 (0) = 0
So, x = - 1 and x = 2 are zeroes of given polynomial. (v) If x = 0 is a zero of polynomial p(x) = x2 then p(0) should be zero.
Now, p(0) = (0)2 = 0
Hence x = 0 is a zero of given polynomial (vi) If
 (vii) If
(vii) If 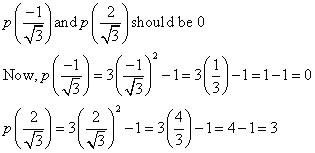 Hence,
Hence, 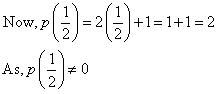 So,
So,
Question 4
Find the zero of the polynomial in each of the following cases: 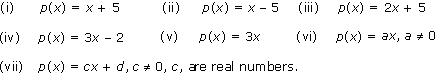
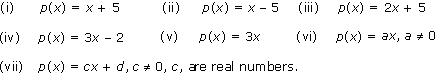
Solution 4
Zero of a polynomial is that value of variable at which value of polynomial comes to 0.
(i) p(x) = x + 5
p(x) = 0
x + 5 = 0
x = - 5
So, for x = - 5, value of polynomial is 0 and hence x = - 5 is a zero of polynomial. (ii) p(x) = x - 5
p(x) = 0
x - 5 = 0
x = 5
So, for x = 5 value of polynomial is 0 and hence x = 5 is a zero of polynomial. (iii) p(x) = 2x + 5
p(x) = 0
2x + 5 = 0
2x = - 5
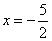
So, for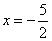 value of polynomial is 0 and hence
value of polynomial is 0 and hence 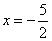 is a zero of polynomial. (iv) p(x) = 3x - 2
is a zero of polynomial. (iv) p(x) = 3x - 2
p(x) = 0
3x - 2 = 0
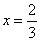
So, for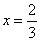 , value of polynomial is 0 and hence
, value of polynomial is 0 and hence 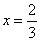 is a zero of polynomial. (v) p(x) = 3x
is a zero of polynomial. (v) p(x) = 3x
p(x) = 0
3x = 0
x = 0
So, for x = 0 value of polynomial is 0 and hence x = 0 is a zero of polynomial. (vi) p(x) = ax
p(x) = 0
ax = 0
x = 0
So, for x = 0, value of polynomial is 0. Hence x = 0 is a zero of polynomial. (vii) p(x) = cx + d
p(x) = 0
cx+ d = 0
 So, for
So, for  , value of polynomial is 0. Hence
, value of polynomial is 0. Hence  is a zero of polynomial. Concept Insight: Equate the polynomial to zero and solve the corresponding linear equation to get the value of variable. Be careful while transposing the terms to the other side. For verification substitute the value of the variable obtained in the polynomial.
is a zero of polynomial. Concept Insight: Equate the polynomial to zero and solve the corresponding linear equation to get the value of variable. Be careful while transposing the terms to the other side. For verification substitute the value of the variable obtained in the polynomial.
(i) p(x) = x + 5
p(x) = 0
x + 5 = 0
x = - 5
So, for x = - 5, value of polynomial is 0 and hence x = - 5 is a zero of polynomial. (ii) p(x) = x - 5
p(x) = 0
x - 5 = 0
x = 5
So, for x = 5 value of polynomial is 0 and hence x = 5 is a zero of polynomial. (iii) p(x) = 2x + 5
p(x) = 0
2x + 5 = 0
2x = - 5
So, for
p(x) = 0
3x - 2 = 0
So, for
p(x) = 0
3x = 0
x = 0
So, for x = 0 value of polynomial is 0 and hence x = 0 is a zero of polynomial. (vi) p(x) = ax
p(x) = 0
ax = 0
x = 0
So, for x = 0, value of polynomial is 0. Hence x = 0 is a zero of polynomial. (vii) p(x) = cx + d
p(x) = 0
cx+ d = 0
NCERT Solution for Class 9 Mathematics Chapter 2 - Polynomials Page/Excercise 2.3
Question 1
Find the remainder when x3 + 3x2 + 3x + 1 is divided by 

Solution 1
Let p(x) = x3 + 3x2 + 3x + 1. (i) x + 1
Zero of x +1 is-1.
i.e. p(-1) = (- 1)3 + 3 (- 1)2 + 3 (-1) + 1 = 0
So, the remainder is 0. (ii)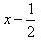 Zero of
Zero of 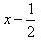 is
is 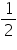
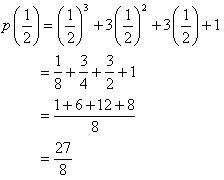 (iii) x
(iii) x
Zero of x is 0.
p(0) = (0)3 + 3(0)2 + 3(0) + 1 = 1
So, the remainder is 1. (iv) x +
Zero of x + is:
is:
x + = 0
= 0 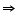 x = -
x = - 
p (- ) = (-
) = (-  )3 + 3(-
)3 + 3(-  )2 + 3(-
)2 + 3(-  ) + 1 = -
) + 1 = -  3 + 3
3 + 3  2 - 3
2 - 3 + 1
+ 1
So, the remainder is - 3 + 3
3 + 3  2 - 3
2 - 3 + 1 (v) 5 + 2x
+ 1 (v) 5 + 2x
Zero of 5+2x is:
5 + 2x = 0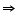 2x = - 5
2x = - 5
i.e. x = -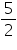
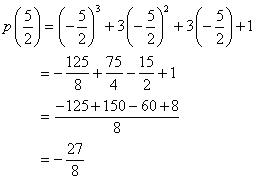 OR (i) x + 1 By long division
OR (i) x + 1 By long division 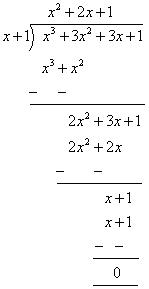 So, remainder is 0. (ii).
So, remainder is 0. (ii). 
By long division
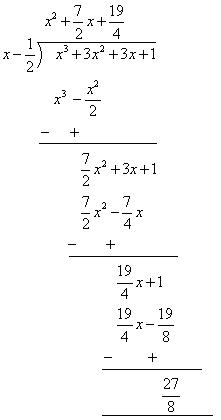 So, remainder is
So, remainder is 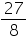 . (iii) x By long division
. (iii) x By long division 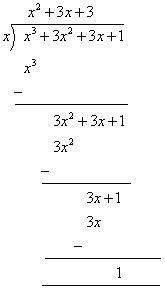 So, remainder is 1. (iv) x +
So, remainder is 1. (iv) x + 
By long division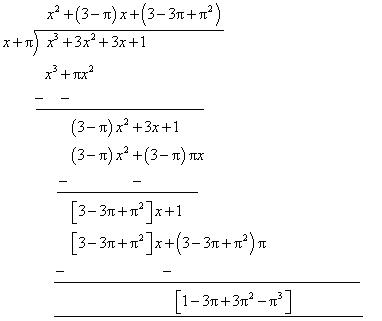 So, the remainder is
So, the remainder is  (v) 5 + 2x
(v) 5 + 2x
By long division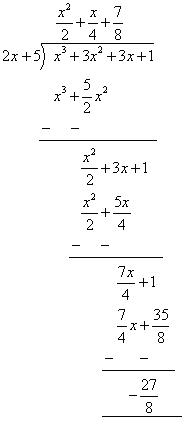 So the remainder is -
So the remainder is -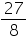 . Concept Insight: The remainder of any polynomial p(x) when divided by another polynomial (ax+b) where a and b are real numbers
. Concept Insight: The remainder of any polynomial p(x) when divided by another polynomial (ax+b) where a and b are real numbers 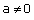 is p(-b/a).
is p(-b/a).
Note that here -b/a is the zero of polynomial ax+b.
This problem can also be solved using long division. For long division first write the divisor and dividend in the standard form, i.e. arrange the terms in the descending order of their powers. The process of division is continued till the remainder is constant or the degree of new dividend is less than the degree of divisor. Do not forget to change the sign of terms while subtraction. For cross verification division algorithm
Dividend = Quotient Divisor + Remainder can be used.
Divisor + Remainder can be used.
Zero of x +1 is-1.
i.e. p(-1) = (- 1)3 + 3 (- 1)2 + 3 (-1) + 1 = 0
So, the remainder is 0. (ii)
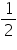
 (iii) x
(iii) xZero of x is 0.
p(0) = (0)3 + 3(0)2 + 3(0) + 1 = 1
So, the remainder is 1. (iv) x +

Zero of x +
 is:
is: x +
 = 0
= 0  x = -
x = - 
p (-
 ) = (-
) = (-  )3 + 3(-
)3 + 3(-  )2 + 3(-
)2 + 3(-  ) + 1 = -
) + 1 = -  3 + 3
3 + 3  2 - 3
2 - 3 + 1
+ 1So, the remainder is -
 3 + 3
3 + 3  2 - 3
2 - 3 + 1 (v) 5 + 2x
+ 1 (v) 5 + 2xZero of 5+2x is:
5 + 2x = 0
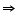 2x = - 5
2x = - 5i.e. x = -
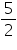
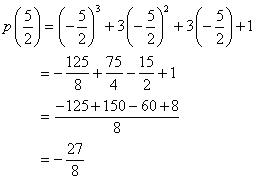 OR (i) x + 1 By long division
OR (i) x + 1 By long division 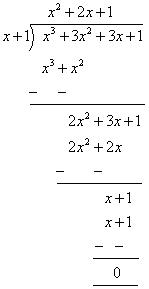 So, remainder is 0. (ii).
So, remainder is 0. (ii). By long division
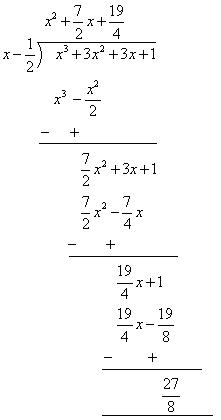 So, remainder is
So, remainder is 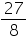 . (iii) x By long division
. (iii) x By long division 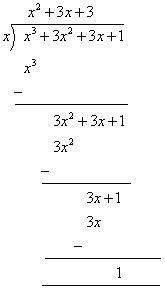 So, remainder is 1. (iv) x +
So, remainder is 1. (iv) x + 
By long division
 So, the remainder is
So, the remainder is By long division
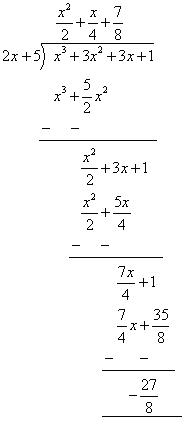 So the remainder is -
So the remainder is -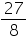 . Concept Insight: The remainder of any polynomial p(x) when divided by another polynomial (ax+b) where a and b are real numbers
. Concept Insight: The remainder of any polynomial p(x) when divided by another polynomial (ax+b) where a and b are real numbers Note that here -b/a is the zero of polynomial ax+b.
This problem can also be solved using long division. For long division first write the divisor and dividend in the standard form, i.e. arrange the terms in the descending order of their powers. The process of division is continued till the remainder is constant or the degree of new dividend is less than the degree of divisor. Do not forget to change the sign of terms while subtraction. For cross verification division algorithm
Dividend = Quotient
 Divisor + Remainder can be used.
Divisor + Remainder can be used.
Question 2
Find the remainder when x3 - ax2 + 6x - a is divided by x - a.
Solution 2
According to the remainder theorem, if p(x) is any polynomial of degree  1 and a is any real number, then when p(x) is divided by the linear polynomial x - a, then the remainder is p(a).
1 and a is any real number, then when p(x) is divided by the linear polynomial x - a, then the remainder is p(a).
Here p(x) = x3 - ax2 + 6x - a
p(a) = (a)3 - a(a)2 + 6a - a
= 5a
So when x3 - ax2 + 6x - a is divided by x - a, remainder comes to 5a. OR
By long division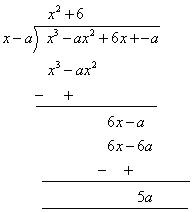 So when x3 - ax2 + 6x - a is divided by x - a, remainder comes to 5a. Concept Insight: The remainder of any polynomial p(x) when divided by another polynomial (ax+b) where a and b are real numbers
So when x3 - ax2 + 6x - a is divided by x - a, remainder comes to 5a. Concept Insight: The remainder of any polynomial p(x) when divided by another polynomial (ax+b) where a and b are real numbers 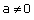 is
is
p(-b/a).
Note that here -b/a is the zero of polynomial ax+ b.
This question can also be solved using long division method however it is long and time consuming. Chances of making computational error are high in that method.
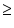 1 and a is any real number, then when p(x) is divided by the linear polynomial x - a, then the remainder is p(a).
1 and a is any real number, then when p(x) is divided by the linear polynomial x - a, then the remainder is p(a).Here p(x) = x3 - ax2 + 6x - a
p(a) = (a)3 - a(a)2 + 6a - a
= 5a
So when x3 - ax2 + 6x - a is divided by x - a, remainder comes to 5a. OR
By long division
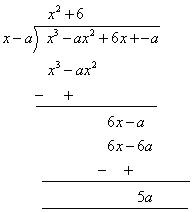 So when x3 - ax2 + 6x - a is divided by x - a, remainder comes to 5a. Concept Insight: The remainder of any polynomial p(x) when divided by another polynomial (ax+b) where a and b are real numbers
So when x3 - ax2 + 6x - a is divided by x - a, remainder comes to 5a. Concept Insight: The remainder of any polynomial p(x) when divided by another polynomial (ax+b) where a and b are real numbers p(-b/a).
Note that here -b/a is the zero of polynomial ax+ b.
This question can also be solved using long division method however it is long and time consuming. Chances of making computational error are high in that method.
Question 3
Check whether 7 + 3x is a factor of 3x3 + 7x.
Solution 3
Zero of 7 + 3x is:
7 + 3x = 0
Therefore,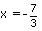 7+3x can be a factor of p(x) = 3x3 + 7x only if
7+3x can be a factor of p(x) = 3x3 + 7x only if 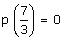
Here p(x) = 3x3 + 7x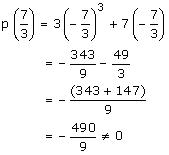
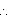 7 + 3x is not a factor of 3x3 + 7x. OR Let us divide (3x3 + 7x) by (7 + 3x). If remainder comes out to be 0 then 7 + 3x will be a factor of 3x3 + 7x.
7 + 3x is not a factor of 3x3 + 7x. OR Let us divide (3x3 + 7x) by (7 + 3x). If remainder comes out to be 0 then 7 + 3x will be a factor of 3x3 + 7x.
By long division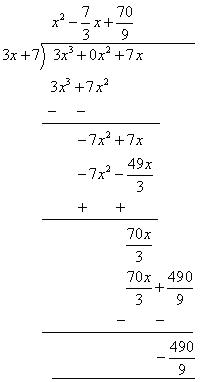 As remainder is not zero so 7 + 3x is not a factor of 3x3 + 7x.
As remainder is not zero so 7 + 3x is not a factor of 3x3 + 7x.
Concept Insight: Any linear polynomial 'ax+b' where a and b are real numbers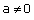 is a factor of the polynomial p(x) iff p(-b/a) = 0 i.e -b/a is a zero of p(x) or both the polynomials has a common zero -b/a. This question can also be solved using long division method. Do not forget to change the sign of terms while subtraction in the long division.
is a factor of the polynomial p(x) iff p(-b/a) = 0 i.e -b/a is a zero of p(x) or both the polynomials has a common zero -b/a. This question can also be solved using long division method. Do not forget to change the sign of terms while subtraction in the long division.
7 + 3x = 0
Therefore,
Here p(x) = 3x3 + 7x
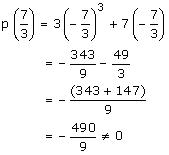
By long division
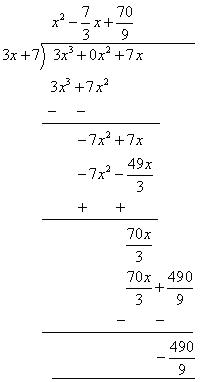 As remainder is not zero so 7 + 3x is not a factor of 3x3 + 7x.
As remainder is not zero so 7 + 3x is not a factor of 3x3 + 7x.Concept Insight: Any linear polynomial 'ax+b' where a and b are real numbers
NCERT Solution for Class 9 Mathematics Chapter 2 - Polynomials Page/Excercise 2.4
Question 1
Determine which of the following polynomials has (x + 1) as a factor: 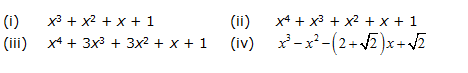
Solution 1
(i) If (x + 1) is a factor of p(x) = x3 + x2 + x + 1, p (- 1) must be zero.
Here, p(x) = x3 + x2 + x + 1
p(-1) = (- 1)3 + (- 1)2 + (- 1) + 1
= - 1 + 1 - 1 + 1 = 0
Hence, x + 1 is a factor of this polynomial (ii) If (x + 1) is a factor of p(x) = x4 + x3 + x2 + x + 1, p (- 1) must be zero.
Here, p(x) = x4 + x3 + x2 + x + 1
p( -1) = (- 1)4 + (- 1)3 + (- 1)2 + (- 1) + 1
= 1 - 1 + 1 -1 + 1 = 1
As,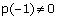 So, x + 1 is not a factor of this polynomial (iii) If (x + 1) is a factor of polynomial p(x) = x4 + 3x3 + 3x2 + x + 1, p(- 1) must be 0.
So, x + 1 is not a factor of this polynomial (iii) If (x + 1) is a factor of polynomial p(x) = x4 + 3x3 + 3x2 + x + 1, p(- 1) must be 0.
p(- 1) = (- 1)4 + 3(- 1)3 + 3(- 1)2 + (- 1) + 1
= 1 - 3 + 3 - 1 + 1 = 1
As,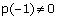 So, x + 1 is not a factor of this polynomial (iv) If (x + 1) is a factor of polynomial
So, x + 1 is not a factor of this polynomial (iv) If (x + 1) is a factor of polynomial
p(x) =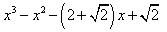 , p(- 1) must be 0.
, p(- 1) must be 0.
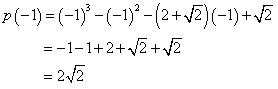
As,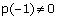
So, (x + 1) is not a factor of this polynomial. Concept Insight: A linear polynomial 'x-a' is a factor of the polynomial p(x) iff p(a) = 0. Note that 'a' is a zero of polynomials x-a and p(x) . Be careful while squaring and cubing the numbers.
Here, p(x) = x3 + x2 + x + 1
p(-1) = (- 1)3 + (- 1)2 + (- 1) + 1
= - 1 + 1 - 1 + 1 = 0
Hence, x + 1 is a factor of this polynomial (ii) If (x + 1) is a factor of p(x) = x4 + x3 + x2 + x + 1, p (- 1) must be zero.
Here, p(x) = x4 + x3 + x2 + x + 1
p( -1) = (- 1)4 + (- 1)3 + (- 1)2 + (- 1) + 1
= 1 - 1 + 1 -1 + 1 = 1
As,
p(- 1) = (- 1)4 + 3(- 1)3 + 3(- 1)2 + (- 1) + 1
= 1 - 3 + 3 - 1 + 1 = 1
As,
p(x) =
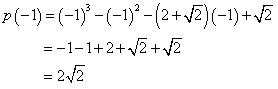
As,
So, (x + 1) is not a factor of this polynomial. Concept Insight: A linear polynomial 'x-a' is a factor of the polynomial p(x) iff p(a) = 0. Note that 'a' is a zero of polynomials x-a and p(x) . Be careful while squaring and cubing the numbers.
Question 2
Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:
(i) p(x) = 2x3 + x2 - 2x - 1, g(x) = x + 1
(ii) p(x) = x3 + 3x2 + 3x + 1, g(x) = x + 2
(iii) p(x) = x3 - 4 x2 + x + 6, g(x) = x - 3
(i) p(x) = 2x3 + x2 - 2x - 1, g(x) = x + 1
(ii) p(x) = x3 + 3x2 + 3x + 1, g(x) = x + 2
(iii) p(x) = x3 - 4 x2 + x + 6, g(x) = x - 3
Solution 2
(i) If g(x) = x + 1 is a factor of given polynomial p(x), p(- 1) must be zero.
p(x) = 2x3 + x2 - 2x - 1
p(- 1) = 2(- 1)3 + (- 1)2 - 2(- 1) - 1
= 2(- 1) + 1 + 2 - 1 = 0
Hence, g(x) = x + 1 is a factor of given polynomial. (ii) If g(x) = x + 2 is a factor of given polynomial p(x), p(- 2) must be 0.
p(x) = x3 +3x2 + 3x + 1
p(- 2) = (- 2)3 + 3(- 2)2 + 3(- 2) + 1
= - 8 + 12 - 6 + 1
= - 1
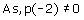
Hence g(x) = x + 2 is not a factor of given polynomial. (iii) If g(x) = x - 3 is a factor of given polynomial p(x), p(3) must be 0.
p(x) = x3 - 4 x2 + x + 6
p(3) = (3)3 - 4(3)2 + 3 + 6
= 27 - 36 + 9 = 0
So, g(x) = x - 3 is a factor of given polynomial. Concept Insight: The problem is a direct application of Factor theorem. g(x) will be the factor of the polynomial p(x) iff the zero of the linear polynomial g(x) when put in place of the variable of polynomial results to zero. Be careful while squaring and cubing the numbers.
p(x) = 2x3 + x2 - 2x - 1
p(- 1) = 2(- 1)3 + (- 1)2 - 2(- 1) - 1
= 2(- 1) + 1 + 2 - 1 = 0
Hence, g(x) = x + 1 is a factor of given polynomial. (ii) If g(x) = x + 2 is a factor of given polynomial p(x), p(- 2) must be 0.
p(x) = x3 +3x2 + 3x + 1
p(- 2) = (- 2)3 + 3(- 2)2 + 3(- 2) + 1
= - 8 + 12 - 6 + 1
= - 1
Hence g(x) = x + 2 is not a factor of given polynomial. (iii) If g(x) = x - 3 is a factor of given polynomial p(x), p(3) must be 0.
p(x) = x3 - 4 x2 + x + 6
p(3) = (3)3 - 4(3)2 + 3 + 6
= 27 - 36 + 9 = 0
So, g(x) = x - 3 is a factor of given polynomial. Concept Insight: The problem is a direct application of Factor theorem. g(x) will be the factor of the polynomial p(x) iff the zero of the linear polynomial g(x) when put in place of the variable of polynomial results to zero. Be careful while squaring and cubing the numbers.
Question 3
Find the value of k, if x - 1 is a factor of p(x) in each of the following cases: 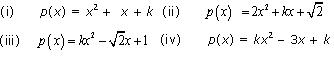
Solution 3
If x - 1 is a factor of polynomial p(x), then p(1) = 0 (i) p(x) = x2 + x + k
p(1) = 0
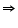 (1)2 + 1 + k = 0
(1)2 + 1 + k = 0
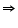 2 + k = 0
2 + k = 0
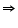 k = - 2
k = - 2
So, value of k is - 2.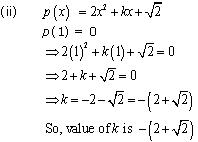
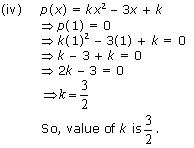 Concept Insight: x-1 is a factor of the given polynomial p(x) iff p(1) = 0 thus equating p(1) to zero will give the required value of constant k. Be careful with arithmetic simplifications.
Concept Insight: x-1 is a factor of the given polynomial p(x) iff p(1) = 0 thus equating p(1) to zero will give the required value of constant k. Be careful with arithmetic simplifications.
p(1) = 0
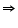 (1)2 + 1 + k = 0
(1)2 + 1 + k = 0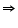 2 + k = 0
2 + k = 0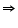 k = - 2
k = - 2So, value of k is - 2.
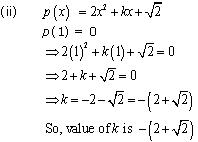
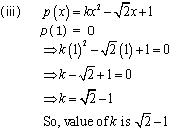
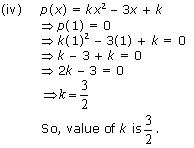 Concept Insight: x-1 is a factor of the given polynomial p(x) iff p(1) = 0 thus equating p(1) to zero will give the required value of constant k. Be careful with arithmetic simplifications.
Concept Insight: x-1 is a factor of the given polynomial p(x) iff p(1) = 0 thus equating p(1) to zero will give the required value of constant k. Be careful with arithmetic simplifications.
Question 4
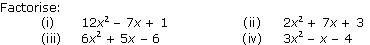
Solution 4
(i) 12x2 - 7x + 1
The two numbers such that pq = 12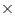 1 = 12 and p + q = - 7. They are p = - 4 and q = - 3
1 = 12 and p + q = - 7. They are p = - 4 and q = - 3
Now, 12x2 - 7x + 1 = 12x2 - 4x - 3x + 1
= 4x (3x - 1) - 1 (3x - 1)
= (3x - 1) (4x - 1) (ii) 2x2 + 7x + 3
The two numbers such that pq = 2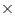 3 = 6 and p + q = 7.
3 = 6 and p + q = 7.
They are p = 6 and q = 1
Now, 2x2 + 7x + 3 = 2x2 + 6x + x + 3
= 2x (x + 3) + 1 (x + 3)
= (x + 3) (2x+ 1) (iii) 6x2 + 5x - 6
The two numbers such that pq = - 36 and p + q = 5.
They are p = 9 and q = - 4
Now,
6x2 + 5x - 6 = 6x2 + 9x - 4x - 6
= 3x (2x + 3) - 2 (2x + 3)
= (2x + 3) (3x - 2)
(iv) 3x2 - x - 4
The two numbers such that pq = 3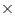 (- 4) = - 12 and p + q = - 1.
(- 4) = - 12 and p + q = - 1.
They are p = - 4 and q = 3.
Now,
3x2 - x - 4 = 3x2 - 4x + 3x - 4
= x (3x - 4) + 1 (3x - 4)
= (3x - 4) (x + 1)
Concept Insight: To factorise the polynomial ax2+bx+c, by splitting the middle term,
b is expressed as the sum of two numbers whose product is ac.
Do not forget to consider the sign of the terms while splitting.
Remember
The two numbers such that pq = 12
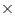 1 = 12 and p + q = - 7. They are p = - 4 and q = - 3
1 = 12 and p + q = - 7. They are p = - 4 and q = - 3Now, 12x2 - 7x + 1 = 12x2 - 4x - 3x + 1
= 4x (3x - 1) - 1 (3x - 1)
= (3x - 1) (4x - 1) (ii) 2x2 + 7x + 3
The two numbers such that pq = 2
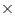 3 = 6 and p + q = 7.
3 = 6 and p + q = 7.They are p = 6 and q = 1
Now, 2x2 + 7x + 3 = 2x2 + 6x + x + 3
= 2x (x + 3) + 1 (x + 3)
= (x + 3) (2x+ 1) (iii) 6x2 + 5x - 6
The two numbers such that pq = - 36 and p + q = 5.
They are p = 9 and q = - 4
Now,
6x2 + 5x - 6 = 6x2 + 9x - 4x - 6
= 3x (2x + 3) - 2 (2x + 3)
= (2x + 3) (3x - 2)
(iv) 3x2 - x - 4
The two numbers such that pq = 3
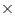 (- 4) = - 12 and p + q = - 1.
(- 4) = - 12 and p + q = - 1. They are p = - 4 and q = 3.
Now,
3x2 - x - 4 = 3x2 - 4x + 3x - 4
= x (3x - 4) + 1 (3x - 4)
= (3x - 4) (x + 1)
Concept Insight: To factorise the polynomial ax2+bx+c, by splitting the middle term,
b is expressed as the sum of two numbers whose product is ac.
Do not forget to consider the sign of the terms while splitting.
Remember
ac>0
|
b>0
|
b =(p+q) where p>0,q>0
|
ac>0
|
b<0
|
b =(p+q) where p<0,q<0
|
ac<0
|
b>0
|
b =(p+q) where
p > q then p>0 and q<0 |
ac<0
|
b<0
|
b =(p+q) where
p > q then p<0 and q>0 |
Question 5
Factorise: (i) x3 - 2x2 - x + 2 (ii) x3 - 3x2 - 9x - 5 (iii) x3 + 13x2 + 32x + 20 (iv) 2y3 + y2 - 2y - 1
Solution 5
(i) Let p(x) = x3 - 2x2 - x + 2
Factors of 2 are � 1, � 2.
By hit and trial method
p(2) = (2)3 - 2(2)2 - 2 + 2
= 8 - 8 - 2 + 2 = 0
So, (x - 2) is factor of polynomial p(x)
By long division Now, Dividend = Divisor
Now, Dividend = Divisor 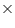 Quotient + Remainder
Quotient + Remainder
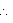 x3 - 2x2 - x + 2 = (x + 1) (x2 - 3x + 2) + 0
x3 - 2x2 - x + 2 = (x + 1) (x2 - 3x + 2) + 0
= (x + 1) [x2 - 2x - x + 2]
= (x + 1) [x (x - 2) - 1 (x - 2)]
= (x + 1) (x - 1) (x - 2)
= (x - 2) (x - 1) (x + 1) (ii) Let p(x) = x3 - 3x2 - 9x - 5
Factors of 5 are �1, � 5.
By hit and trial method
p(- 1) = (- 1)3 - 3(- 1)2 - 9(- 1) - 5
= - 1 - 3 + 9 - 5 = 0
So x + 1 is a factor of this polynomial
Let us find the quotient while dividing x3 + 3x2 - 9x - 5 by x + 1
By long division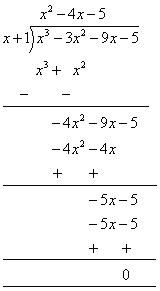 Now, Dividend = Divisor
Now, Dividend = Divisor  Quotient + Remainder
Quotient + Remainder
 x3 - 3x2 - 9x - 5 = (x + 1) (x2 - 4 x - 5) + 0
x3 - 3x2 - 9x - 5 = (x + 1) (x2 - 4 x - 5) + 0
= (x + 1) (x2 - 5 x + x - 5)
= (x + 1) [(x (x - 5) +1 (x - 5)]
= (x + 1) (x - 5) (x + 1)
= (x - 5) (x + 1) (x + 1) (iii) Let p(x) = x3 + 13x2 + 32x + 20
The factors of 20 are �1, � 2, � 4, � 5 ... ...
By hit and trial method
p(- 1) = (- 1)3 + 13(- 1)2 + 32(- 1) + 20
= - 1 + 13 - 32 + 20
= 33 - 33 = 0
As p(-1) is zero, so x + 1 is a factor of this polynomial p(x).
Let us find the quotient while dividing x3 + 13x2 + 32x + 20 by (x + 1)
By long division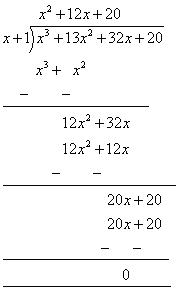 We know that
We know that
Dividend = Divisor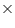 Quotient + Remainder
Quotient + Remainder
x3 + 13x2 + 32x + 20 = (x + 1) (x2 + 12x + 20) + 0
= (x + 1) (x2 + 10x + 2x + 20)
= (x + 1) [x (x + 10) + 2 (x + 10)]
= (x + 1) (x + 10) (x + 2)
= (x + 1) (x + 2) (x + 10) (iv) Let p(y) = 2y3 + y2 - 2y - 1
By hit and trial method
p(1) = 2 ( 1)3 + (1)2 - 2( 1) - 1
= 2 + 1 - 2 - 1= 0
So, y - 1 is a factor of this polynomial
By long division method,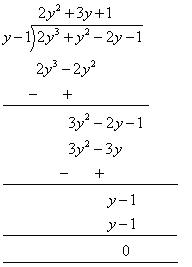 p(y) = 2y3 + y2 - 2y - 1
p(y) = 2y3 + y2 - 2y - 1
= (y - 1) (2y2 +3y + 1)
= (y - 1) (2y2 +2y + y +1)
= (y - 1) [2y (y + 1) + 1 (y + 1)]
= (y - 1) (y + 1) (2y + 1)
Concept Insight: To factorise p(x) when its degree is greater than or equal to 3 note down all the factors of constant term considering both negative and positive sign.
Check the obtained factors for the possible zeroes of the polynomial p(x) Using Factor theorem one zero can be obtained continue the process till all the zeroes are obtained or use long division method. To obtain the other quadratic factor use long division to determine the other factors. The degree of the polynomial is less than or equal to the number of real factors the polynomial.
Factors of 2 are � 1, � 2.
By hit and trial method
p(2) = (2)3 - 2(2)2 - 2 + 2
= 8 - 8 - 2 + 2 = 0
So, (x - 2) is factor of polynomial p(x)
By long division
 Now, Dividend = Divisor
Now, Dividend = Divisor  Quotient + Remainder
Quotient + Remainder= (x + 1) [x2 - 2x - x + 2]
= (x + 1) [x (x - 2) - 1 (x - 2)]
= (x + 1) (x - 1) (x - 2)
= (x - 2) (x - 1) (x + 1) (ii) Let p(x) = x3 - 3x2 - 9x - 5
Factors of 5 are �1, � 5.
By hit and trial method
p(- 1) = (- 1)3 - 3(- 1)2 - 9(- 1) - 5
= - 1 - 3 + 9 - 5 = 0
So x + 1 is a factor of this polynomial
Let us find the quotient while dividing x3 + 3x2 - 9x - 5 by x + 1
By long division
 Now, Dividend = Divisor
Now, Dividend = Divisor 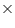 Quotient + Remainder
Quotient + Remainder= (x + 1) (x2 - 5 x + x - 5)
= (x + 1) [(x (x - 5) +1 (x - 5)]
= (x + 1) (x - 5) (x + 1)
= (x - 5) (x + 1) (x + 1) (iii) Let p(x) = x3 + 13x2 + 32x + 20
The factors of 20 are �1, � 2, � 4, � 5 ... ...
By hit and trial method
p(- 1) = (- 1)3 + 13(- 1)2 + 32(- 1) + 20
= - 1 + 13 - 32 + 20
= 33 - 33 = 0
As p(-1) is zero, so x + 1 is a factor of this polynomial p(x).
Let us find the quotient while dividing x3 + 13x2 + 32x + 20 by (x + 1)
By long division
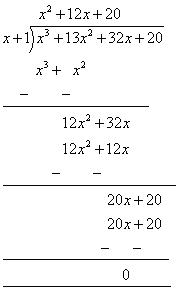 We know that
We know thatDividend = Divisor
 Quotient + Remainder
Quotient + Remainderx3 + 13x2 + 32x + 20 = (x + 1) (x2 + 12x + 20) + 0
= (x + 1) (x2 + 10x + 2x + 20)
= (x + 1) [x (x + 10) + 2 (x + 10)]
= (x + 1) (x + 10) (x + 2)
= (x + 1) (x + 2) (x + 10) (iv) Let p(y) = 2y3 + y2 - 2y - 1
By hit and trial method
p(1) = 2 ( 1)3 + (1)2 - 2( 1) - 1
= 2 + 1 - 2 - 1= 0
So, y - 1 is a factor of this polynomial
By long division method,
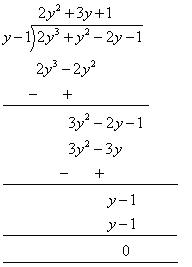 p(y) = 2y3 + y2 - 2y - 1
p(y) = 2y3 + y2 - 2y - 1= (y - 1) (2y2 +3y + 1)
= (y - 1) (2y2 +2y + y +1)
= (y - 1) [2y (y + 1) + 1 (y + 1)]
= (y - 1) (y + 1) (2y + 1)
Concept Insight: To factorise p(x) when its degree is greater than or equal to 3 note down all the factors of constant term considering both negative and positive sign.
Check the obtained factors for the possible zeroes of the polynomial p(x) Using Factor theorem one zero can be obtained continue the process till all the zeroes are obtained or use long division method. To obtain the other quadratic factor use long division to determine the other factors. The degree of the polynomial is less than or equal to the number of real factors the polynomial.
NCERT Solution for Class 9 Mathematics Chapter 2 - Polynomials Page/Excercise 2.5
Question 1
Use suitable identities to find the following products: 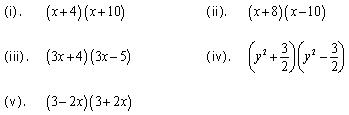
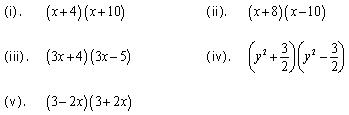
Solution 1
(i). By using identity 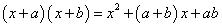
 (ii). By using identity
(ii). By using identity 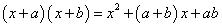
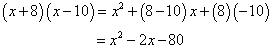 (iii).
(iii).  By using the identity
By using the identity 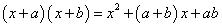
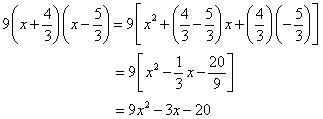 (iv). By using identity
(iv). By using identity 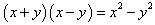
 (v). By using identity
(v). By using identity 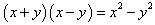
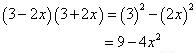 Concept Insight: If the value of the two terms of the binomials are equal then use the algebraic identity (x+a) (x-a) = x2 - a2 else use (x+a) (x+b) = x2+(a+b)x+ab to obtain required product.
Concept Insight: If the value of the two terms of the binomials are equal then use the algebraic identity (x+a) (x-a) = x2 - a2 else use (x+a) (x+b) = x2+(a+b)x+ab to obtain required product.
 (ii). By using identity
(ii). By using identity 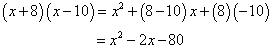 (iii).
(iii). 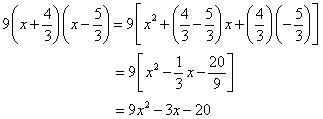 (iv). By using identity
(iv). By using identity  (v). By using identity
(v). By using identity 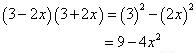 Concept Insight: If the value of the two terms of the binomials are equal then use the algebraic identity (x+a) (x-a) = x2 - a2 else use (x+a) (x+b) = x2+(a+b)x+ab to obtain required product.
Concept Insight: If the value of the two terms of the binomials are equal then use the algebraic identity (x+a) (x-a) = x2 - a2 else use (x+a) (x+b) = x2+(a+b)x+ab to obtain required product.
Question 2
Evaluate the following products without multiplying directly:
(i) 103  107 (ii) 95
107 (ii) 95  96 (iii) 104
96 (iii) 104  96
96
(i) 103
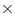 107 (ii) 95
107 (ii) 95 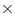 96 (iii) 104
96 (iii) 104 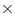 96
96
Solution 2
(i). 103 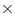 107 = (100 + 3) (100 + 7)
107 = (100 + 3) (100 + 7)
= (100)2 + (3 + 7) 100 + (3) (7)
[By using the identity,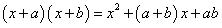 , where
, where
x = 100, a = 3 and b = 7]
= 10000 + 1000 + 21
= 11021 (ii). 95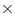 96 = (100 - 5) (100 - 4)
96 = (100 - 5) (100 - 4)
= (100)2 + (- 5 - 4) 100 + (- 5) (- 4)
[By using the identity,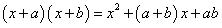 , where
, where
x = 100, a = - 5 and b = - 4]
= 10000 - 900 + 20
= 9120 (iii). 104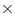 96 = (100 + 4) (100 - 4)
96 = (100 + 4) (100 - 4)
= (100)2 - (4)2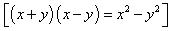
= 10000 - 16
= 9984 Concept Insight: The key is to use the algebraic identity (x+a) (x+b) = x2+(a+b)x+ab or (x+a) (x-a) = x2 - a2 for such questions. Write each of the numeral as 100 � k , or any other suitable number whose square can be easily computed.
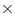 107 = (100 + 3) (100 + 7)
107 = (100 + 3) (100 + 7)= (100)2 + (3 + 7) 100 + (3) (7)
[By using the identity,
x = 100, a = 3 and b = 7]
= 10000 + 1000 + 21
= 11021 (ii). 95
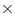 96 = (100 - 5) (100 - 4)
96 = (100 - 5) (100 - 4)= (100)2 + (- 5 - 4) 100 + (- 5) (- 4)
[By using the identity,
x = 100, a = - 5 and b = - 4]
= 10000 - 900 + 20
= 9120 (iii). 104
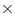 96 = (100 + 4) (100 - 4)
96 = (100 + 4) (100 - 4)= (100)2 - (4)2
= 10000 - 16
= 9984 Concept Insight: The key is to use the algebraic identity (x+a) (x+b) = x2+(a+b)x+ab or (x+a) (x-a) = x2 - a2 for such questions. Write each of the numeral as 100 � k , or any other suitable number whose square can be easily computed.
Question 3
Factorise the following using appropriate identities: 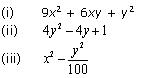
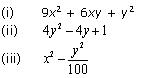
Solution 3
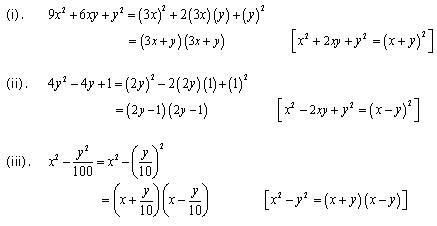 Concept Insight: Use the appropriate square identity. If the polynomial has only two terms, reduce each term to the perfect square and use the algebraic identity
Concept Insight: Use the appropriate square identity. If the polynomial has only two terms, reduce each term to the perfect square and use the algebraic identity
Question 4
Expand each of the following, using suitable identities: 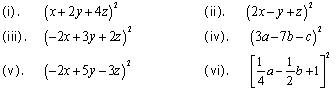
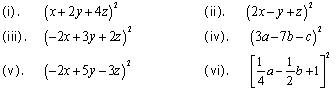
Solution 4
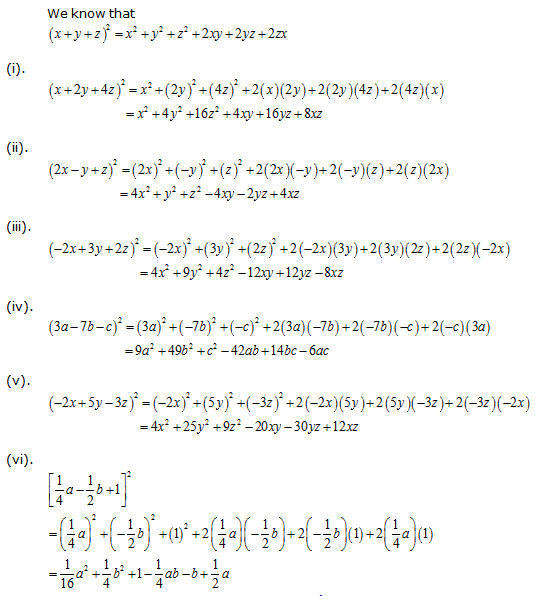 Concept Insight: Use the algebraic identity
Concept Insight: Use the algebraic identity
Question 5
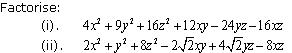
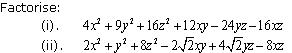
Solution 5
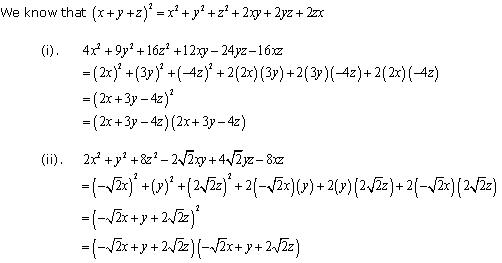 Concept Insight: Use the algebraic identity
Concept Insight: Use the algebraic identity
Question 6
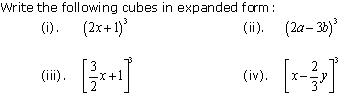
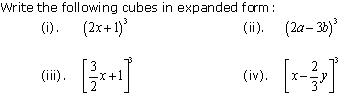
Solution 6
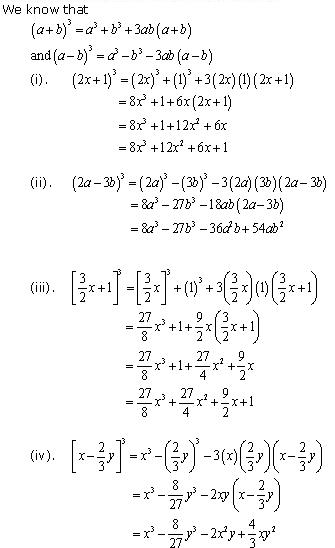 Concept Insight: Since the expressions involves cube so cubic identity will be used. If the terms of the given polynomial are separated by positive sign use the identity
Concept Insight: Since the expressions involves cube so cubic identity will be used. If the terms of the given polynomial are separated by positive sign use the identity
Question 7
Evaluate the following using suitable identities:
(i). (99)3 (ii). (102)3 (iii). (998)3
(i). (99)3 (ii). (102)3 (iii). (998)3
Solution 7
We know that 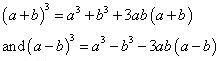 (i) (99)3 = (100 - 1)3
(i) (99)3 = (100 - 1)3
= (100)3 - (1)3 - 3(100) (1) (100 - 1)
= 1000000 - 1 - 300(99)
= 1000000 - 1 - 29700
= 970299
(ii) (102)3 = (100 + 2)3
= (100)3 + (2)3 + 3(100) (2) (100 + 2)
= 1000000 + 8 + 600 (102)
= 1000000 + 8 + 61200
= 1061208
(iii) (998)3 = (1000 - 2)3
= (1000)3 - (2)3 - 3(1000) (2) (1000 - 2)
= 1000000000 - 8 - 6000(998)
= 1000000000 - 8 - 5988000
= 1000000000 - 5988008
= 994011992 Concept Insight: Use the cubic identity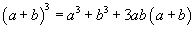 and
and 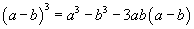 . Write the numerical term as something added or subtracted from 10,100, 1000 or higher powers of 10 as it's easy to compute higher powers of 10. Carefully apply the mathematical operations.
. Write the numerical term as something added or subtracted from 10,100, 1000 or higher powers of 10 as it's easy to compute higher powers of 10. Carefully apply the mathematical operations.
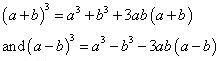 (i) (99)3 = (100 - 1)3
(i) (99)3 = (100 - 1)3= (100)3 - (1)3 - 3(100) (1) (100 - 1)
= 1000000 - 1 - 300(99)
= 1000000 - 1 - 29700
= 970299
(ii) (102)3 = (100 + 2)3
= (100)3 + (2)3 + 3(100) (2) (100 + 2)
= 1000000 + 8 + 600 (102)
= 1000000 + 8 + 61200
= 1061208
(iii) (998)3 = (1000 - 2)3
= (1000)3 - (2)3 - 3(1000) (2) (1000 - 2)
= 1000000000 - 8 - 6000(998)
= 1000000000 - 8 - 5988000
= 1000000000 - 5988008
= 994011992 Concept Insight: Use the cubic identity
Question 8
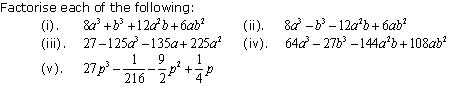
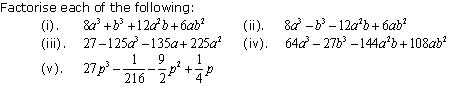
Solution 8
 Concept Insight: Since all the polynomial given here have degree 3 so cubic identities would be used here. Now if all the terms of the given polynomial are positive then use identity
Concept Insight: Since all the polynomial given here have degree 3 so cubic identities would be used here. Now if all the terms of the given polynomial are positive then use identity
Question 9


Solution 9
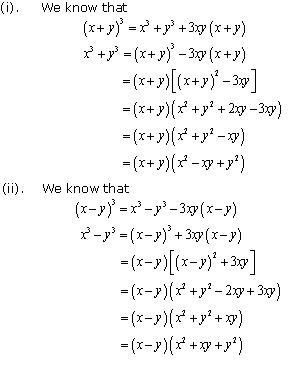 Concept Insight: When the two terms of the polynomial are separated by positive sign use the identity
Concept Insight: When the two terms of the polynomial are separated by positive sign use the identity
Question 10
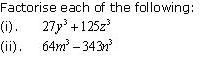
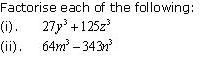
Solution 10
 Concept Insight: Reduce the terms of the polynomial to perfect cube and then if the two terms of the polynomial are separated by positive sign use the identity
Concept Insight: Reduce the terms of the polynomial to perfect cube and then if the two terms of the polynomial are separated by positive sign use the identity
Question 11
Factorise: 27x3 + y3 + z3 -9xyz
Solution 11
We Know that 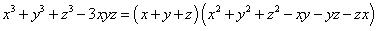
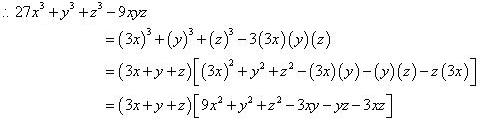 Concept Insight: Reduce each terms of the polynomial as per the left hand side of the standard identity,
Concept Insight: Reduce each terms of the polynomial as per the left hand side of the standard identity, 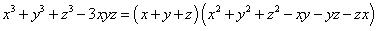 .
.
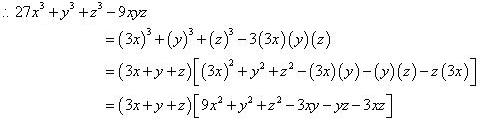 Concept Insight: Reduce each terms of the polynomial as per the left hand side of the standard identity,
Concept Insight: Reduce each terms of the polynomial as per the left hand side of the standard identity,
Question 12
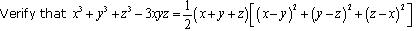
Solution 12
We know that 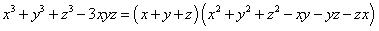
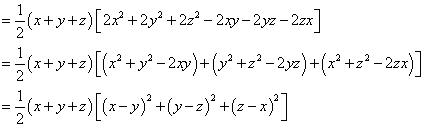 Concept Insight: Since the left hand side of the identity resembles the left hand side of identity,
Concept Insight: Since the left hand side of the identity resembles the left hand side of identity, 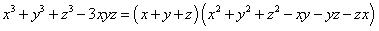 , so this identity will be applicable here. Now the right hand side of the above identity can be written into many forms we need to look at what is required to proved, Accordingly apply mathematical simplifications and square identities to get the desired result.
, so this identity will be applicable here. Now the right hand side of the above identity can be written into many forms we need to look at what is required to proved, Accordingly apply mathematical simplifications and square identities to get the desired result.
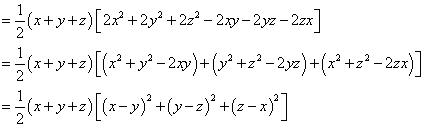 Concept Insight: Since the left hand side of the identity resembles the left hand side of identity,
Concept Insight: Since the left hand side of the identity resembles the left hand side of identity,
Question 13
If x + y + z = 0, show that x3 + y3 + z3 = 3xyz
Solution 13
 Concept Insight: Use the result that
Concept Insight: Use the result that
Question 14
Without actually calculating the cubes, find the value of each of the following: 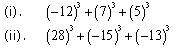
Solution 14
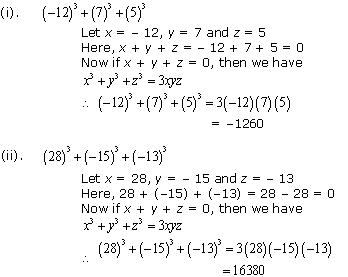 Concept Insight: Use the result
Concept Insight: Use the result
Question 15
Give possible expressions for the length and breadth of each of the following rectangle, in which their areas are given: 

Solution 15
We know that,
Area = length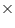 breadth
breadth 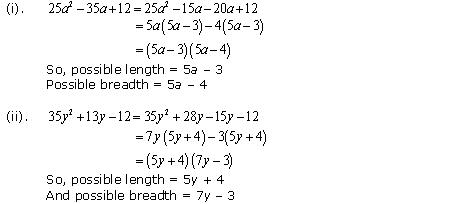 Concept Insight: For such questions factorise the expression, given for the area of rectangle by splitting the middle term. One of its factors will be its length and the other will be its breadth.
Concept Insight: For such questions factorise the expression, given for the area of rectangle by splitting the middle term. One of its factors will be its length and the other will be its breadth.
Area = length
 breadth
breadth  Concept Insight: For such questions factorise the expression, given for the area of rectangle by splitting the middle term. One of its factors will be its length and the other will be its breadth.
Concept Insight: For such questions factorise the expression, given for the area of rectangle by splitting the middle term. One of its factors will be its length and the other will be its breadth.
Question 16
What are the possible expressions for the dimensions of the cuboids whose volumes are given below? 

Solution 16
We know that,
Volume of cuboid = length breadth
breadth  height (i).
height (i). 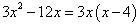
So, the possible solutions is
Length = 3, breadth = x, height = x - 4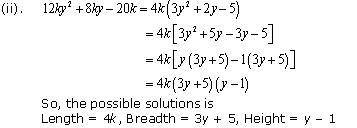 Concept Insight: For such questions factorise the expression, given for the volume of the cuboid by taking the common term out if it has two terms and by splitting the middle term if the polynomial has three terms. Three factors obtained will be its length breadth and height.
Concept Insight: For such questions factorise the expression, given for the volume of the cuboid by taking the common term out if it has two terms and by splitting the middle term if the polynomial has three terms. Three factors obtained will be its length breadth and height.
Volume of cuboid = length
 breadth
breadth  height (i).
height (i). So, the possible solutions is
Length = 3, breadth = x, height = x - 4
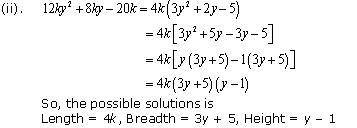 Concept Insight: For such questions factorise the expression, given for the volume of the cuboid by taking the common term out if it has two terms and by splitting the middle term if the polynomial has three terms. Three factors obtained will be its length breadth and height.
Concept Insight: For such questions factorise the expression, given for the volume of the cuboid by taking the common term out if it has two terms and by splitting the middle term if the polynomial has three terms. Three factors obtained will be its length breadth and height.
No comments:
Post a Comment